Метод последовательных уступок.
Рассмотрим один из методов, использующих ограничения на критерии – метод последовательных уступок. Алгоритм метода следующий:
1. Критерии нумеруются в порядке убывания важности.
2. Решается задача
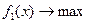
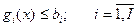 ;
;
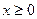 .
.
Определяется значение 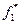 .
.
3. Устанавливается уступка 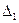 , по этому критерию.
, по этому критерию.
4. Решается задача
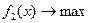
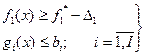 ;
;
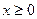 .
.
Если в задаче более двух критериев, то пункты 3 и 4 повторяются для 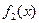 ,...,
,..., 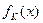 .
.
Субоптимальный план, найденный при решении последней задачи, является оптимальным компромиссным планом в данной схеме компромисса.
Метод последовательных уступок, являясь простым и понятным в реализации, обладает, тем не менее, целым рядом недостатков, основными из которых являются:
1. Сложность и субъективизм в ранжировании критериев.
2. Субъективизм в задании величин уступок.
3. Степени достижения оптимума (безусловного) по всем критериям, кроме первого, не определены. Рассчитать их можно, лишь решив исходные модели по соответствующим целевым функциям (еще (k - 1) задач) на глобальный оптимум.
4. Поскольку уступка по последнему критерию не делается, степень достижения оптимума по нему может оказаться совершенно неудовлетворительной. Для «исправления» плана в этом случае вес расчеты должны быть повторены с другими (причем не гарантирующими нужных окончательных результатов) коэффициентами уступок.
Пример. Решить задачу методом последовательных уступок, если уступка по первому критерию составляет 10% от его оптимального значения.
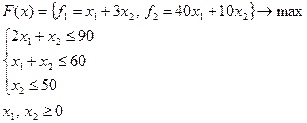
Решение.
Решим задачу по критерию 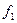 . Получим
. Получим 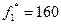 . В соответствии с условием задачи величина уступки
. В соответствии с условием задачи величина уступки 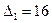 . Дополнительное ограничение будет иметь вид
. Дополнительное ограничение будет иметь вид 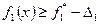 , то есть
, то есть 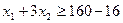 . Решая задачу
. Решая задачу
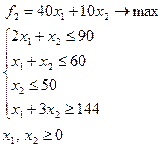
получим 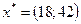 ,
, 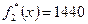 ,
, 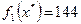
Задача 1.
Предприятие может выпускать пять видов продукции И1, И2, ИЗ, И4, И5. Для этого используется три вида ресурсов, расход которых на производство единицы продукции и их запасы приведены в таблице:
| Ресурс | И1 | И2 | ИЗ | И4 | И5 | Запасы |
| В1 | ||||||
| В2 | ||||||
| В3 |
Все изделия обрабатываются на станках четырех типов. Норма времени на обработку одного изделия и фонд времени работы станков приведены в таблице:
| Вид станков | И1 | И2 | И3 | И4 | И5 | Фонд времени (ст./час) |
| Станок 1 | ||||||
| Станок 2 | ||||||
| Станок 3 | ||||||
| Станок 4 |
Оптовая цена и себестоимость единицы продукции соответствующего типа приведены в таблице:
| И1 | И2 | И3 | И4 | И5 | |
| Оптовая цена (ден.ед.) | |||||
| Себестоимость(ден.ед.) |
Объем каждого вида продукции должен быть не менее 100 и не более 500 единиц. Мерой эффективности производственной программы являются следующие показатели:
1. Прибыль предприятия – f1;
2. Валовый объем выпуска продукции в стоимостном выражении – f2;
3. Себестоимость продукции – f3;
4. Уровень загрузки оборудования – f4.
Требуется.
1. Решить задачу методом последовательных уступок, если уступку по каждому критерию полагать равной 10% от его оптимального значения.
2. Решить задачу методом свертывания критериев, выбрав вектор весовых коэффициентов методом парных сравнений.
Решение.
1. Составим ЭММ задачи.
Обозначим через 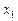 – количество продукции И1,
– количество продукции И1, 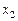 – количество продукции И2,
– количество продукции И2, 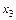 – количество продукции И3,
– количество продукции И3, 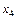 – количество продукции И4,
– количество продукции И4, 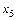 – количество продукции И5.
– количество продукции И5.
Целевые функции будут иметь вид:
Прибыль: 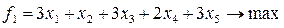 .
.
Валовый объем ( в стоимостном выражении):
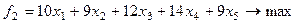 .
.
Себестоимость: 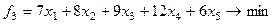 .
.
Уровень загрузки оборудования: 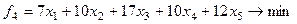
Ограничениями задачи будут:
1). По расходу ресурсов:
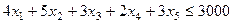 – В1
– В1
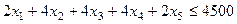 – В2
– В2
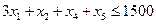 – В3
– В3
2). По фонду времени работы оборудования:
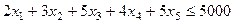
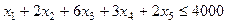
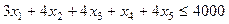
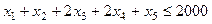
3). По объему выпускаемой продукции: 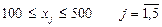 .
.
4). Условие целочисленности переменных: 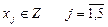 .
.
Пронормируйте критерии.
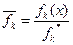
Для этого необходимо сначала найти оптимальные решения задачи 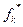 по каждому критерию в отдельности.
по каждому критерию в отдельности.
Дата добавления: 2016-01-20; просмотров: 5919;
