Комплексная мощность

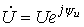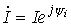Активную, реактивную и полную мощности можно определить, пользуясь комплексными изображениями напряжения и тока. Пусть , а . Тогда комплекс полной мощности:

,

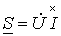(9)

где 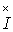- комплекс, сопряженный с комплексом .

.

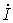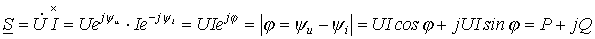Комплексной мощности можно поставить в соответствие треугольник мощностей (см. рис. 4). Рис. 4 соответствует 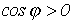(активно-индуктивная нагрузка), для которого имеем:

.

Применение статических конденсаторов для повышения cos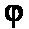

Как уже указывалось, реактивная мощность 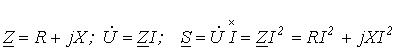циркулирует между источником и потребителем. Реактивный ток, не совершая полезной работы, приводит к дополнительным потерям в силовом оборудовании и, следовательно, к завышению его установленной мощности. В этой связи понятно стремление к увеличению 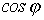в силовых электрических цепях.

Следует указать, что подавляющее большинство потребителей (электродвигатели, электрические печи, другие различные устройства и приборы) как нагрузка носит активно-индуктивный характер.

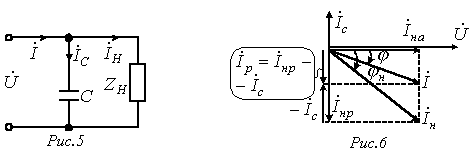
Если параллельно такой нагрузке 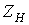(см. рис. 5), включить конденсатор С, то общий ток 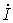, как видно из векторной диаграммы (рис. 6), приближается по фазе к напряжению, т.е. 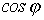увеличивается, а общая величина тока (а следовательно, потери) уменьшается при постоянстве активной мощности . На этом основано применение конденсаторов для повышения .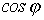

Какую емкость С нужно взять, чтобы повысить коэффициент мощности от значения 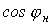до значения ?

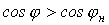Разложим 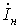на активную 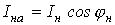и реактивную 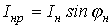составляющие. Ток через конденсатор 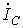компенсирует часть реактивной составляющей тока нагрузки :

;

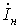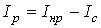(10)

;

(11)

.

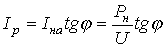(12)

Из (11) и (12) с учетом (10) имеем

,

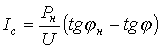но , откуда необходимая для повышения 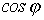емкость:

.

(13)

Баланс мощностей

Баланс мощностей является следствием закона сохранения энергии и может служить критерием правильности расчета электрической цепи.

а) Постоянный ток

Для любой цепи постоянного тока выполняется соотношение:

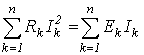
(14)

Это уравнение представляет собой математическую форму записи баланса мощностей: суммарная мощность, генерируемая источниками электрической энергии, равна суммарной мощности, потребляемой в цепи.

Следует указать, что в левой части (14) слагаемые имеют знак “+”, поскольку активная мощность рассеивается на резисторах. В правой части (14) сумма слагаемых больше нуля, но отдельные члены здесь могут иметь знак “-”, что говорит о том, что соответствующие источники работают в режиме потребителей энергии (например, заряд аккумулятора).

б) Переменный ток.

Из закона сохранения энергии следует, что сумма всех отдаваемых активных мощностей равна сумме всех потребляемых активных мощностей, т.е.

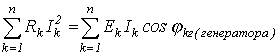
(15)

В ТОЭ доказывается (вследствие достаточной громоздкости вывода это доказательство опустим), что баланс соблюдается и для реактивных мощностей:

,

(16)

где знак “+” относится к индуктивным элементам , “-” – к емкостным .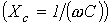

Умножив (16) на “j” и сложив полученный результат с (15), придем к аналитическому выражению баланса мощностей в цепях синусоидального тока (без учета взаимной индуктивности):

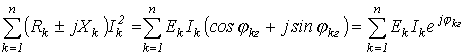
или

.

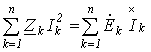Литература

1. Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
2. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.

Контрольные вопросы и задачи

1. Что такое активная мощность?
2. Что такое реактивная мощность, с какими элементами она связана?
3. Что такое полная мощность?
4. Почему необходимо стремиться к повышению коэффициента мощности ?
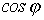5. Критерием чего служит баланс мощностей?
6. К источнику с напряжением подключена активно-индуктивная нагрузка, ток в которой 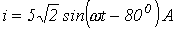. Определить активную, реактивную и полную мощности.

Ответ: Р=250 Вт; Q=433 ВАр; S=500 ВА.

1. В ветви, содержащей последовательно соединенные резистор R и катушку индуктивности L, ток I=2 A. Напряжение на зажимах ветви U=100 B, а потребляемая мощность Р=120 Вт. Определить сопротивления R и XL элементов ветви.

Ответ: R=30 Ом; XL=40 Ом.

1. Мощность, потребляемая цепью, состоящей из параллельно соединенных конденсатора и резистора, Р=90 Вт. Ток в неразветвленной части цепи I1=5 A, а в ветви с резистором I2=4 A. Определить сопротивления R и XL элементов цепи.

Ответ: R=10 Ом; XС=7,5 Ом.

Лекция N 8