Метод узловых потенциалов в матричной форме
На основании полученного выше соотношения (4), представляющего собой, как было указано, матричную запись закона Ома, запишем матричное выражение:
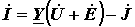 , ,
| (14) |
где 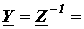
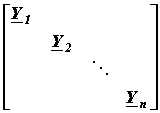 - диагональная матрица проводимостей ветвей, все члены которой, за исключением элементов главной диагонали, равны нулю.
- диагональная матрица проводимостей ветвей, все члены которой, за исключением элементов главной диагонали, равны нулю.
МатрицыZ и Y взаимно обратны.
Умножив обе части равенства (14) на узловую матрицуАи учитывая первый закон Кирхгофа, согласно которому
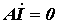 , ,
| (15) |
получим:
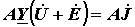 . . . .
| (16) |
Выражение (16) перепишем, как:
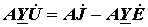 . .
| (17) |
Принимая потенциал узла, для которого отсутствует строка в матрице А, равным нулю, определим напряжения на зажимах ветвей:
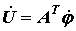 . .
| (18) |
Тогда получаем матричное уравнение вида:
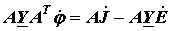 . .
| (19) |
Данное уравнение представляет собой узловые уравнения в матричной форме. Если обозначить
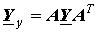
| (20) |
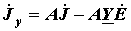 , ,
| (21) |
то получим матричную форму записи уравнений, составленных по методу узловых потенциалов:
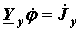
| (22) |
где 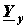 - матрица узловых проводимостей;
- матрица узловых проводимостей; 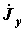 - матрица узловых токов.
- матрица узловых токов.
В развернутом виде соотношение (22) можно записать, как:
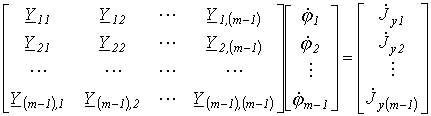
| (23) |
то есть получили известный из метода узловых потенциалов результат.
Рассмотрим составление узловых уравнений на примере схемы по рис. 4.
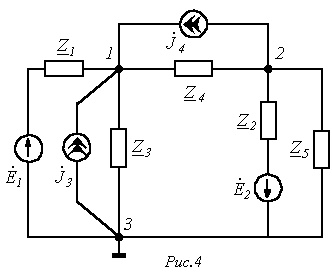
| 
|
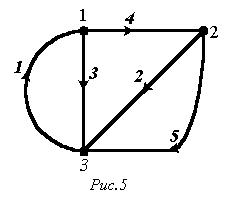
Данная схема имеет 3 узла (m=3) и 5 ветвей (n=5). Граф схемы с выбранной ориентацией ветвей представлен на рис. 5.
Узловая матрица (примем 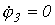 )
)
| А | 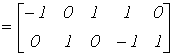
|
Диагональная матрица проводимостей ветвей:
| Y | 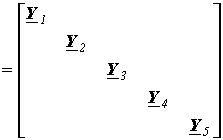 , ,
|
где 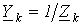 .
.
Матрица узловых проводимостей
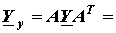
| 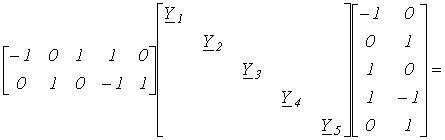
|
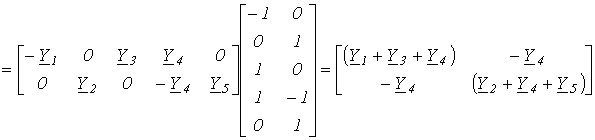 .
.
Матрицы токов и ЭДС источников
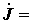
| 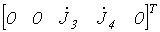
|
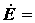
| 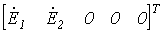
|
. .Следовательно, матрица узловых токов будет иметь вид:
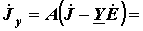
| 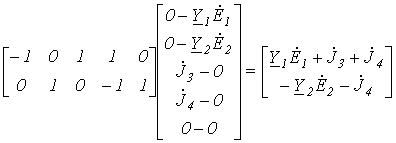
|
.Таким образом, окончательно получаем:
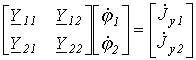 ,
,
где 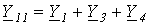 ;
; 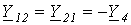 ;
; 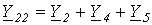 ;
; 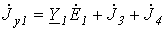 ;
; 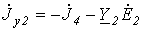 .
.
Анализ результатов показывает, что полученные уравнения идентичны тем, которые можно записать непосредственно из рассмотрения схемы по известным правилам составления уравнений по методу узловых потенциалов.
Литература
- Основытеории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А.Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
- В чем заключаются преимуществаиспользования матричныхметодоврасчета цепей?
- Запишите выражения матрицы контурных сопротивлений и матрицы контурных ЭДС.
- Запишите выражения матрицы узловых проводимостей и матрицы узловых токов.
- Составить узловые уравнения для цепи на рис. 2.
Ответ:
.
- Составить контурные уравнения для цепи рис. 4, приняв, что дерево образовано ветвями 3 и 4 (см. рис. 5).
Ответ:
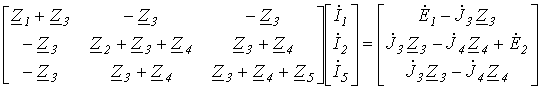 .
.
Лекция N 7
Дата добавления: 2015-11-28; просмотров: 1337;
