Метод узловых потенциалов. Данный метод вытекает из первого закона Кирхгофа
Данный метод вытекает из первого закона Кирхгофа. В качестве неизвестных принимаются потенциалы узлов, по найденным значениям которых с помощью закона Ома для участка цепи с источником ЭДС затем находят токи в ветвях. Поскольку потенциал – величина относительная, потенциал одного из узлов (любого) принимается равным нулю. Таким образом, число неизвестных потенциалов, а следовательно, и число уравнений равно 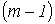 , т.е. числу ветвей дерева
, т.е. числу ветвей дерева  .
.
Пусть имеем схему по рис. 4, в которой примем  .
.
 Допустим, что
Допустим, что 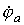 и
и  известны. Тогда значения токов на основании закона Ома для участка цепи с источником ЭДС
известны. Тогда значения токов на основании закона Ома для участка цепи с источником ЭДС
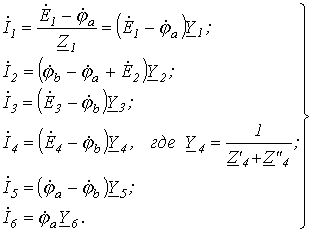
Запишем уравнение по первому закону Кирхгофа для узла а:
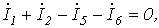
и подставим значения входящих в него токов, определенных выше:
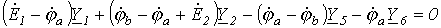 .
.
Сгруппировав соответствующие члены, получим:
 .
.
Аналогично можно записать для узла b:
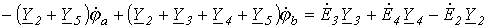 .
.
Как и по методу контурных токов, система уравнений по методу узловых потенциалов может быть составлена формальным путем. При этом необходимо руководствоваться следующими правилами:
1. В левой части i-гоуравнения записывается со знаком “+”потенциал 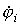 i-го узла, для которого составляется данное i-е уравнение, умноженный на сумму проводимостей
i-го узла, для которого составляется данное i-е уравнение, умноженный на сумму проводимостей  ветвей, присоединенных к данному i-му узлу, и со знаком “-”потенциал
ветвей, присоединенных к данному i-му узлу, и со знаком “-”потенциал 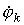 соседних узлов, каждый из которых умножен на сумму проводимостей
соседних узлов, каждый из которых умножен на сумму проводимостей 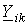 ветвей, присоединенных к i-му иk-му узлам.
ветвей, присоединенных к i-му иk-му узлам.
Из сказанного следует, что все члены 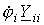 , стоящие на главной диагонали в левой части системы уравнений, записываются со знаком “+”, а все остальные – со знаком “-”, причем
, стоящие на главной диагонали в левой части системы уравнений, записываются со знаком “+”, а все остальные – со знаком “-”, причем 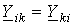 . Последнее равенство по аналогии с методом контурных токов обеспечивает симметрию коэффициентов уравнений относительно главной диагонали.
. Последнее равенство по аналогии с методом контурных токов обеспечивает симметрию коэффициентов уравнений относительно главной диагонали.
2. В правой части i-гоуравнения записывается так называемый узловой ток 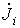 , равный сумме произведений ЭДС ветвей, подходящих к i-му узлу, и проводимостей этих ветвей. При этом член суммы записывается со знаком “+”, если соответствующая ЭДС направлена к i-му узлу, в противном случае ставится знак “-”. Если в подходящих к i-му узлу ветвях содержатся источники тока, то знаки токов источников токов, входящих в узловой ток простыми слагаемыми, определяются аналогично.
, равный сумме произведений ЭДС ветвей, подходящих к i-му узлу, и проводимостей этих ветвей. При этом член суммы записывается со знаком “+”, если соответствующая ЭДС направлена к i-му узлу, в противном случае ставится знак “-”. Если в подходящих к i-му узлу ветвях содержатся источники тока, то знаки токов источников токов, входящих в узловой ток простыми слагаемыми, определяются аналогично.
В заключение отметим, что выбор того или иного из рассмотренных методов определяется тем, что следует найти, а также тем, какой из них обеспечивает меньший порядок системы уравнений. При расчете токов при одинаковом числе уравнений предпочтительнее использовать метод контурных токов, так как он не требует дополнительных вычислений с использованием закона Ома. Метод узловых потенциалов очень удобен при расчетах многофазных цепей, но не удобен при расчете цепей со взаимной индуктивностью.
Литература
1. Основытеории цепей: Учеб.для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
2. Бессонов Л.А.Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с
.
Контрольные вопросы и задачи
1. В ветви на рис. 1 

 . Определить ток
. Определить ток 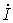 .
.
Ответ: 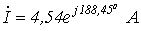 .
.
2. В чем заключается сущность символического метода расчета цепей синусоидального тока?
3. В чем состоит сущность метода контурных токов?
4. В чем состоит сущность метода узловых потенциалов?
5. В цепи на рис. 5 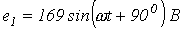 ;
; 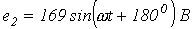 ;
; 
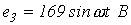 ;
; 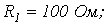
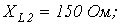
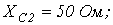
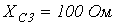 . Методом контурных токов определить комплексы действующих значений токов ветвей.
. Методом контурных токов определить комплексы действующих значений токов ветвей.
Ответ: 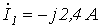 ;
; 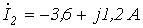 ;
; 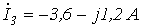 .
.
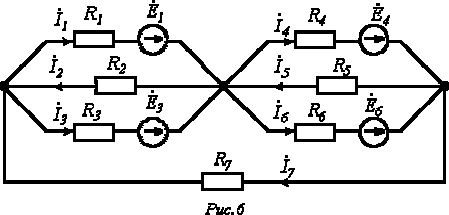
6. В цепи на рис. 6 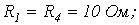
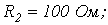
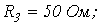
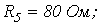
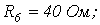
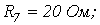
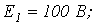
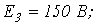
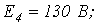
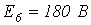 . Рассчитать токи в ветвях, используя метод узловых потенциалов.
. Рассчитать токи в ветвях, используя метод узловых потенциалов.
Ответ: 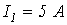 ;
; 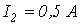 ;
; 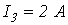 ;
; 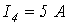 ;
; 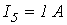 ;
; 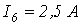 ;
; 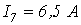 .
.
Лекция N 6
Дата добавления: 2015-11-28; просмотров: 754;
