МГНОВЕННАЯ МОЩНОСТЬ И ЭНЕРГИЯ
Положим, что через участок электрической цепи (приемник энергии) под воздействием приложенного напряжения u проходит электрический заряд q. Совершаемая при этом элементарная работа или, что то же, поступающая в приемник элементарная энергия равна
dw = udq = uidt.
Производная энергии по времени, т.е. скорость поступления в цепь электрической энергии в данный момент времени, представляет собой мгновенную мощность. Следовательно, мгновенная мощность, поступающая в приемник, равна произведению мгновенных значений напряжения и тока
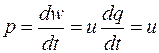 i.
i.
Мгновенная мощность p - величина алгебраическая; она положительна при одинаковых знаках u и i и отрицательна при разных знаках u и i.
Если положительные направления для напряжения и тока приняты совпадающими, то при p > 0 энергия поступает в приемник, а при p < 0 энергия возвращается из рассматриваемого участка цепи обратно к источнику.
Энергия, поступившая в приемник за промежуток времени от t1 до t2, выражается интегралом
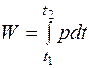 .
.
В отличие от мгновенной мощности p, которая может иметь отрицательный или положительный знак, энергия, поступившая в приемник, всегда имеет положительный знак.
В системе СИ работа и энергия измеряются в джоулях (Дж), мощность p - в ваттах (Вт).
СОПРОТИВЛЕНИЕ
Сопротивлениемназывается идеализированный двухполюсный элемент цепи, характеризующий потери энергии на нагрев, механическую работу или излучение электромагнитной энергии.
Следует заметить, что термин «сопротивление» и соответствующее ему условное обозначение R применяются в электротехнике и радиотехнике для элемента, в котором происходит необратимый процесс поглощения электромагнитной энергии, и для количественной оценки величины, равной отношению напряжения на данном элементе цепи к току, проходящему через него
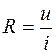 . (1.1)
. (1.1)
Для обозначения физически существующего элемента используется термин резистор.
Здесь предполагается, что положительные направления тока и напряжения совпадают; при этом знаки u и i одинаковы и R > 0.
Величина g = 1/R, обратная сопротивлению, называется проводимостью. В системе СИ сопротивление R измеряется в омах (Ом), а проводимость g - в сименсах (Сим).
Формула (1.1) выражает закон Ома, экспериментально установленный Омом в 1826 г.
Условное графическое изображение сопротивления с указанием выбранных положительных направлений тока и напряжения приведено на рисунке 1.2.

Мгновенная мощность, поступающая в сопротивление, равна произведению мгновенных значений напряжения и тока
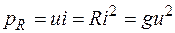 .
.
Следовательно, параметр R может быть численно определен как отношение мгновенной мощности к квадрату мгновенного значения тока, проходящего через сопротивление
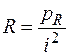 .
.
Электрическая энергия, поступившая в сопротивление и превращенная в тепло, начиная с некоторого момента времени, например t = 0, до рассматриваемого момента t, равна
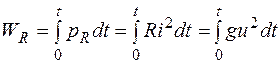 .
.
В случае постоянного тока (i = I = const), 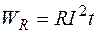 .
.
Превращение всей электрической энергии WR в тепловую впервые было доказано опытным путем Джоулем и Ленцем.
Выделение током теплоты было впервые использовано для целей освещения А. Н. Лодыгиным, создавшим в 1873 г. лампу накаливания (Эдисон изобрел лампу накаливания в 1879 г., после Лодыгина). Оно целенаправленно используется в технике – электронагревательных приборах и т. п. К вредным последствиям теплового действия тока относятся потери электрической энергии в проводах, машинах, аппаратах, порча изоляции проводов от нагрева и т. д.
Параметр R в общем случае зависит от тока i (например, вследствие нагрева резистора током). Зависимость напряжения на резисторе от тока, проходящего через данный резистор, называется вольт-амперной характеристикой, которая в общем случае нелинейна.
Если значение сопротивления R не зависит от величины и направления тока, то имеет место прямая пропорциональность между напряжением и током, выражающая закон Ома. В этом случае сопротивление называется линейным. На рисунке 1.3 показаны вольт-амперные характеристики резистора - нелинейная (кривая а) и линейная (прямая б). В этом разделе рассматриваются линейные резисторы.

Очевидно, величина линейного сопротивления R пропорциональна тангенсу угла наклона прямолинейной вольт-амперной характеристики к оси тока
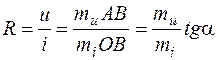 ,
,
где mu и mi - масштабы напряжения (В/мм) и тока (А/мм) на чертеже.
ИНДУКТИВНОСТЬ
Индуктивностьюназывается идеализированный двухполюсный элемент электрической цепи, в котором накапливается энергия магнитного поля. При этом термин «индуктивность» и соответствующее ему условное обозначение L применяются для обозначения элемента цепи, способного накапливать энергию магнитного поля, и для количественной оценки отношения потокосцепления самоиндукции к току в данном элементе
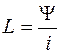 .
.
Для обозначения физически существующего элемента применяется термин катушка индуктивности.
Потокосцеплением самоиндукции цепи называется сумма произведений магнитных потоков, обусловленных только током в этой цепи, на числа витков, с которыми они сцеплены. Если все витки пронизываются одним и тем же магнитным потоком, то потокосцепление равно произведению магнитного потока на число витков.
В Международной системе единиц Ψ измеряется в веберах (Вб), L в генри (Гн). При этом всегда потокосцепление и ток имеют одинаковый знак, так что L > 0.
Зависимость потокосцепления от тока в общем случае нелинейная, и параметр L зависит от тока. В случае, когда характеристика Ψ(i) прямолинейна, индуктивность L постоянна (линейная индуктивность). На рисунке 1.4 показаны нелинейная и линейная зависимости потокосцепления от тока. В этом разделе рассматриваются линейные индуктивности.

На основании закона электромагнитной индукции Фарадея-Максвелла изменение потокосцепления самоиндукции вызывает электродвижущую силу (ЭДС) самоиндукции, которая выражается формулой
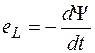 . (1.2)
. (1.2)
По закону Ленца, выражающему принцип электромагнитной инерции, эта ЭДС противодействует изменению потокосцепления, что и учитывается знаком минус в (1.2), поскольку положительное направление для eL выбрано совпадающим с положительным направлением i.
Ввиду совпадения положительных направлений eL и i положительные направления магнитного потока вдоль оси витков и наводимой им ЭДС самоиндукции, точно так же как и положительные направления тока и создаваемого им магнитного потока, связаны правилом правоходового винта.
Условное графическое изображение индуктивности с указанием выбранных положительных направлений тока и ЭДС самоиндукции приведено на рисунке 1.5.
Если L не зависит от i, то предыдущая формула принимает вид
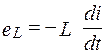 . (1.3)
. (1.3)

Величина
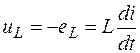 (1.4)
(1.4)
называется падением напряжения в индуктивности, или, что то же, напряжением на индуктивности. Положительное направление uL совпадает с положительным направлением i (рисунок 1.5).
Итак, напряжение на индуктивности пропорционально производной тока по времени. Например, если ток изменяется по закону, изображенному на рисунке 1.6, а, то напряжение на индуктивности представится в виде, приведенном на рисунке 1.6, б (здесь принято L = 3 мГн).
На основании (1.4) ток в индуктивности
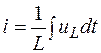 или
или 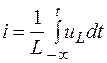 .
.
Нижний предел интеграла принят равным -¥, так как до рассматриваемого момента времени t процесс мог длиться сколь угодно долго.

При t = 0 ток в индуктивности равен
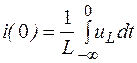 ;
;
следовательно,
 ,
,
т. е. в интервале времени от нуля до t ток в индуктивности изменяется на величину 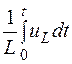 , определяемую площадью, ограниченной в этом интервале кривой напряжения uL.
, определяемую площадью, ограниченной в этом интервале кривой напряжения uL.
Мгновенная мощность, поступающая в индуктивность, равна произведению мгновенных значений напряжения и тока
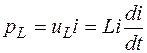 .
.
Она связана с процессом нарастания или убывания энергии магнитного поля. Энергия магнитного поля в произвольный момент времени t определяется по формуле
 . (1.4a)
. (1.4a)
Здесь учтено, что при t = -¥ ток в индуктивности i(-¥) = 0.
Если часть магнитного потока, связанного с индуктивным элементом, связана одновременно и с другим индуктивным элементом, то эти два элемента, кроме параметров L1и L2, обладают параметром М, называемым взаимной индуктивностью. Взаимная индуктивность представляет собой отношение потокосцепления взаимной индукции одного из элементов к току в другом элементе
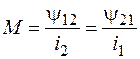 , (1.5)
, (1.5)
здесь Ψ12 – потокосцепление первого элемента, обусловленное током второго элемента;
Ψ21– потокосцепление второго элемента, обусловленное током первого элемента.
В этом случае в первом и во втором элементах наводятся ЭДС взаимной индукции, равные соответственно:
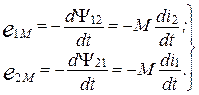 (1.6)
(1.6)
Выражения (1.6) получены в предположении, что М не зависит от i1 и i2, так как здесь рассматриваются линейные цепи.
М измеряется, так же как и L, в Генри. Однако в отличие от параметра L взаимная индуктивность М обозначает не какой-либо самостоятельный элемент электрической цепи, а лишь магнитную связь между индуктивными элементами.
ЕМКОСТЬ
Емкостьюназывается идеализированный двухполюсный элемент электрической цепи, приближенно заменяющий конденсатор, в котором накапливается энергия электрического поля. При этом термин «емкость» и соответствующее ему буквенное обозначение С применяются для обозначения способности накапливать энергию электрического поля и для количественной оценки отношения заряда к напряжению на этом элементе:
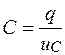 . (1.7)
. (1.7)
Для обозначения физически существующего элемента применяется термин конденсатор.
Если q и uC измеряются в кулонах (К) и вольтах (В), то С измеряется в фарадах (Ф). При этом всегда заряд и напряжение имеют одинаковый знак, так что С > 0.
Зависимость заряда от напряжения в общем случае нелинейна, и, следовательно, параметр С зависит от напряжения.
В случае, когда характеристика q(u) прямолинейна, емкость С постоянна (линейная емкость). На рисунке 1.7 показаны нелинейная и линейная зависимости заряда от напряжения. В этом разделе рассматриваются линейные емкости.

Предположим, что емкость образована двумя пластинами, разделенными диэлектриком. Под влиянием приложенного напряжения на пластинах сосредоточатся равные количества электричества противоположных знаков; пластина с более высоким потенциалом зарядится положительным электричеством, а пластина с более низким потенциалом - отрицательным электричеством.
При изменении напряжения, приложенного к пластинам, изменится в соответствии с (1.7) электрический заряд: к пластине, потенциал которой возрастет, поступит дополнительный положительный заряд, а к пластине, потенциал которой снизится, поступит такой же отрицательный заряд.
Ток равен производной электрического заряда по времени. Поэтому с изменением напряжения на емкости в присоединенной к ней последовательно электрической цепи создается ток, величина которого определяется скоростью изменения заряда на емкости
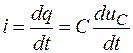 . (1.8)
. (1.8)
Здесь знак заряда q соответствует знаку пластины, к которой направлен ток i.
Этот ток рассматривается как ток проводимости в проводниках, присоединенных к емкостному элементу (ток, обусловленный движением заряженных частиц под действием электрического поля в веществе, обладающем электропроводностью), переходящий в ток смещения в диэлектрике емкостного элемента. Последнее понятие, введенное Максвеллом и применяемое в теории поля, означает скалярную величину, прямо пропорциональную скорости изменения напряженности электрического поля (в случае однородного поля и e = const).
Напомним, что напряженность электрического поля численно определяется силой, действующей на электрический заряд, равный единице.
Благодаря введению понятия тока смещения ток в цепи с емкостью представляется замкнутым через диэлектрик.
Согласно (1.8) ток положителен, когда заряд q и соответственно напряжение uC возрастают.
На основании (1.8) напряжение на емкости
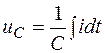 ,
,
или
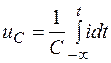 .
.
Здесь, как и в предыдущем параграфе, предполагается, что до рассматриваемого момента времени t процесс мог длиться сколь угодно долго, и поэтому нижний предел интеграла принят равным -¥.
При t = 0 напряжение на емкости равно
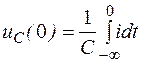 .
.
Следовательно,
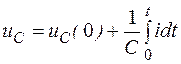 ,
,
т. е. в интервале времени от нуля до t напряжение на емкости изменяется на величину  , определяемую площадью, ограниченной в указанном интервале кривой тока i.
, определяемую площадью, ограниченной в указанном интервале кривой тока i.
Условное графическое изображение емкости с указанием положительных направлений тока и напряжения приведено на рисунке 1.8.

Полярность емкости, указанная на рисунке 1.8 знаками «+» и «-», соответствует положительному напряжению uC, т. е. положительному заряду на пластине «+».
Мгновенная мощность, поступающая в емкость, равна
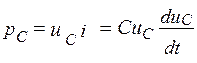 .
.
Она связана с процессом накопления или убыли электрического заряда в емкости.
Когда заряд положителен и возрастает, то ток положителен, и в емкость поступает электрическая энергия из внешней цепи.
Когда заряд положителен, но убывает, т.е. ток отрицателен, энергия, ранее накопленная в электрическом поле емкости, возвращается во внешнюю цепь.
Допустим, что к емкости С приложено некоторое напряжение uC. Энергия электрического поля в произвольный момент времени t определится по формуле
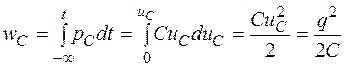 . (1.8a)
. (1.8a)
Здесь учтено, что при t = -¥ напряжение на емкости uC (-¥) = 0.
Дата добавления: 2015-12-16; просмотров: 4916;
