Внутренняя энергия магнетиков

dU = TdS + 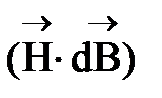. (35)

Свободная энергия магнетика

dF = – SdT + 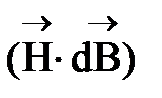. (36)

Термодинамический потенциал

dФ = – SdT – 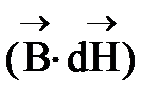. (37)

Энтальпия магнетика

dI = TdS – 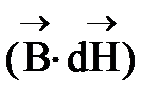. (38)

Уравнение состояния магнетика запишем в виде

В =f(Н, Т, r),

где Н – напряженность внешнего магнитного поля; Т – абсолютная температура; r – плотность магнетика.

Используя уравнение состояния (36) для свободной энергии, получаем следующее выражение:

F = ò 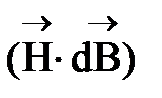+ F₀(Т, r), (39)

где F₀ – значение свободной энергии при отсутствии магнитного поля.

После интегрирования (39) с учетом того, что В = mm₀Н (при Т = const; r = const), имеет

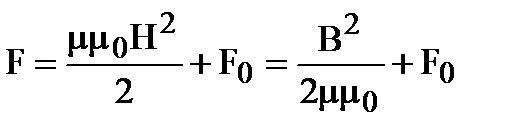. (40)

После интегрирования (35) найдем внутреннюю энергию магнетика:

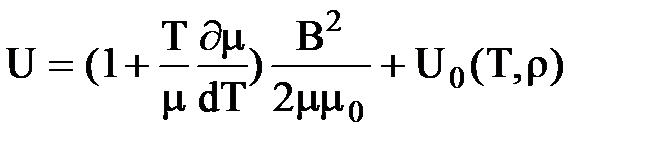, (41)

где U₀ – внутренняя энергия магнетика в отсутствие магнитного поля.

Адиабатическое и квазистатическое изменение намагниченности 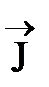приводит к изменению температуры (магнитокалорический эффект).

Из условия постоянства энтропии можно найти изменение температуры, если S = f(T, B); r = const, т. е.

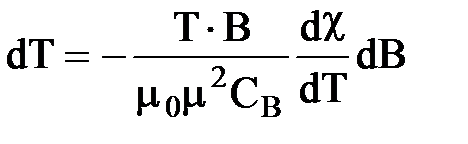, (42)

где С_В – теплоемкость единицы объема магнетика при В = const,

или 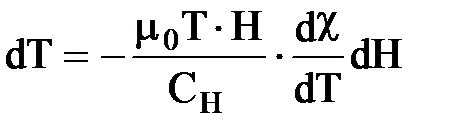, (43)

где С_Н – теплоемкость единицы объема магнетика при Н = const.

Применяя формулу (43) к парамагнетикам с учетом закона Кюри, согласно которому магнитная восприимчивость c парамагнитного образца пропорциональна абсолютной температуре, т. е.

, (44)

Получаем 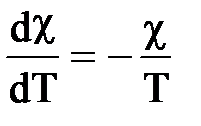. (45)

С учетом этого формула (43) принимает вид

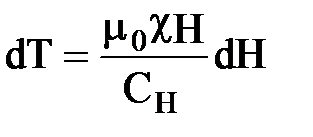. (46)

Следовательно, при обратимом адиабатическом размагничивании парамагнетик охлаждается.