Атом в магнитном поле

При движении электрона вокруг ядра по орбите радиуса r на него действует центростремительная сила

.

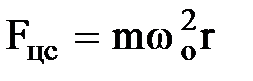Если атом внести во внешнее магнитное поле, вектор индукции 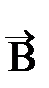которого перпендикулярен плоскости орбиты электрона, то на электрон начнет действовать сила Лоренца

,

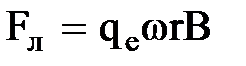где w - круговая частота обращения электрона в магнитном поле.

Уравнение движения электрона в магнитном поле запишем в виде

mw²r = F_цс ± F_л

или

mw²r = ± ,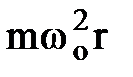

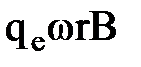где знаки «±» выбираются в соответствии с относительной ориентацией векторов 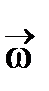и .

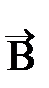После преобразования последнего выражения получим

mr(w - w_o) (w + w_o) = 2mrDw×w = ± q_ewrB,

где Dw =½w-w_o ½<< w; 2w @ w+w_o.

Из последнего выражения найдем, что

w_L = Dw = ±

или в векторном виде

. (7)

Таким образом, в магнитном поле электрон получает дополнительную угловую скорость вращения, которую называют частотой Лармора.

Причем векторы 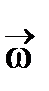_L и 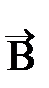cовпадают по направлению (рис.4.12).

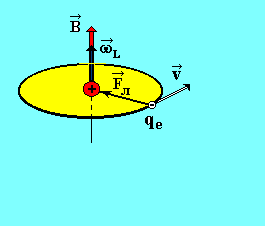Рис. 2

Частоту Лармора приобретают все электроны атома, так как она не зависит от радиуса орбиты и скорости движения электрона.

Скорость электрона при внесении атома в магнитное поле изменяется, поэтому изменяется и его кинетическая энергия W_k.

Но так как радиус вращения остается неизменным, то потенциальная энергия электрона не изменяется.

За счет чего же изменяется энергия электрона в атоме, если магнитное поле действует перпендикулярно скорости и не производит работы?

Частота Лармора возникает в момент включения магнитного поля.

Следовательно, переменное магнитное поле возбуждает переменное электрическое поле, которое и сообщает электрону дополнительное вращение с частотой Лармора.

Таким образом, возникновение ларморовского вращения вызвано проявлением электромагнитной индукции.

Это явление наблюдается во всех без исключения веществах при внесении их в магнитное поле. Векторы 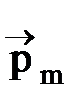и 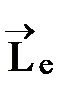начинают прецессировать вокруг направления 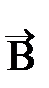с частотой Лармора (вектор 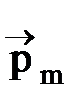описывает коническую поверхность, рис. 2.).

Теорема Лармора: Единственным результатом влияния магнитного поля на орбиту электрона в атоме является прецессия орбиты и вектора 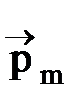с угловой скоростью 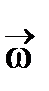_L вокруг оси, проходящей через ядро атома и параллельно вектору индукции 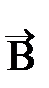внешнего магнитного поля.

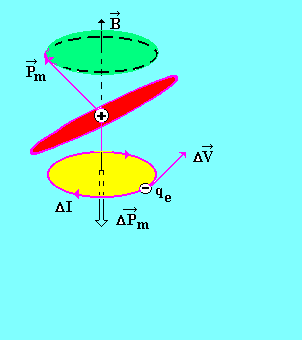Рис. 3

В результате прецессии наводится дополнительный орбитальный магнитный момент электрона, модуль которого

Dр_m = DI×S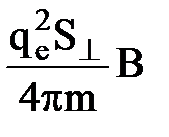_^ = , (8)

где DI = q_eDn, w_L = 2pDn; S_^ - площадь проекции орбиты электрона на плоскость, перпендикулярную 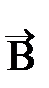(рис. 3).

Так как вектор D 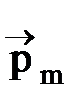противоположен по направлению вектору 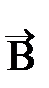, то

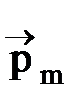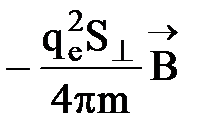D = . (9)

Если атом содержит Z электронов, то наведенный магнитный момент

D 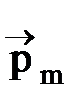= 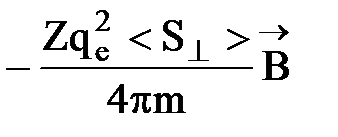, (10)

где < S_^ > - cреднее значение площади S_^ для орбит всех электронов атома.

При суммировании орбитальных и спиновых магнитных моментов атомов может произойти их полная компенсация.

Тогда результирующий магнитный момент атома равен нулю.

Если такой компенсации не происходит, то атом имеет постоянный магнитный момент. Вещества, у которых атомы в отсутствие внешнего магнитного поля имеют постоянный магнитный момент, не равный нулю, могут быть парамагнетиками, ферромагнетиками, антиферромагнетиками или ферримагнетиками.