Движение заряженных частиц в магнитном поле

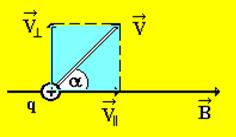Рис. 13

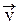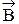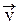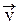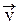Пусть заряженная частица влетает со скоростью в однородное магнитное поле под углом a к силовой линии (рис. 13). Разложим скорость на составляющие _^ и _||, т. е.

= _^ + _||,

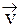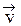где v_^ = vsina, v_|| = vcosa.

На заряженную частицу, движущуюся в магнитном поле, действует сила Лоренца

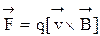(42)

или

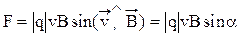. (43)

При a = 0^о F = 0 ( ­­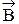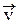 _||), т. е. если заряженная частица движется вдоль силовой линии, на нее не действует сила Лоренца, и она продолжает двигаться равномерно и прямолинейно (v_| =const).

При a = 90^о, 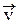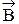_^^ , F = |q| v_^B.

Под действием максимальной силы Лоренца частица описывает окружность радиуса R, т. е. 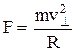, или 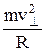= |q| v_^B.

Следовательно,

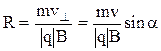. (44)

Заряженная частица движется по окружности равномерно с постоянной угловой скоростью w (В = const, q = const, v_^ = const), поэтому можно найти период ее обращения Т = 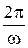, где 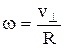, т. е. 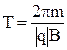. (45)

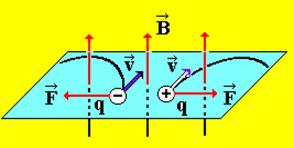Рис. 14

Следовательно, при v << c период обращения частицы по окружности не зависит от скорости ее движения. Направление силы Лоренца зависит не только от направлений вектора скорости 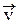_^ и вектора индукции магнитного поля 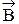, но и от знака движущегося заряда и определяется по правилу правого винта (рис. 14). Участвуя в двух движениях, частица в магнитном поле описывает винтовую кривую вокруг силовой линии (рис. 15), шаг которой

H = v_||T = 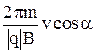. (46)

Если заряженная частица движется в неоднородном магнитном поле в сторону более сильного поля, то она навивается на силовую линию.

А радиус и период обращения уменьшаются. На этом принципе основана магнитная фокусировка пучков заряженных частиц, например, в магнитных линзах в электронной оптике.

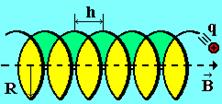Рис. 15

При движении заряженных частиц в электрическом и магнитном полях на них действует обобщенная сила Лоренца, которую можно найти по формуле

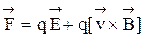, (47)

Влияние электрического и магнитного полей на движущиеся заряженные частицы (электроны, протоны, ядра атомов, ионы и т. д.) применяется в ускорителях заряженных частиц (циклотронах, фазотронах, синхрофазотронах, масс - спектрографах, накопительных кольцах и т. д.). Энергия ускоряемых частиц увеличивается при их движении в электрическом поле (электростатическом, индукционном или переменном высокочастотном). Полученные в ускорителях направленные пучки частиц высоких энергий, используются для решения многих задач ядерной физики.

Эффект Холла

Эффект Холла наблюдается в проводниках и полупроводниках.

Если металлическую (или полупроводниковую) пластинку в форме параллелепипеда, по которой течет электрический ток в направлении от грани 1 к грани 2 поместить в магнитное поле, силовые линии которого пронизывают образец в направлении от грани 3 к грани 4, то на гранях 5 и 6 возникает разность потенциалов (рис. 16).

В металлах носителями тока являются электроны.

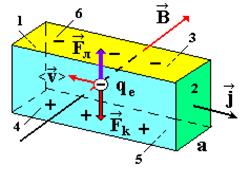Рис. 16

При их концентрации n₀ и скорости упорядоченного движения <v> сила тока

I = q_en₀<v>S, (48)

где S - площадь поперечного сечения пластинки (например, квадрат со стороной a). Для электронов скорость их упорядоченного движения противоположна по направлению вектору плотности тока .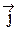

На электроны, движущиеся в магнитном поле с индукцией 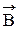, действует сила Лоренца

.

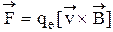В результате этого они отклоняются к верхней грани 6, на которой возникает избыточный отрицательный заряд, а на нижней грани 5 - избыточный положительный заряд.

Возникает разность потенциалов Dj электрического поля, вектор напряженности 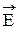которого направлен от грани 5 к грани 6.

Поэтому на электроны будет действовать кулоновская сила, направленная вниз (к грани 5).

В состоянии динамического равновесия полная сила Лоренца, действующая на электроны со стороны электрического и магнитного полей будет равна нулю, т. е.

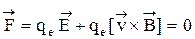
или по модулю

Е = <v>B.

Используя связь разности потенциалов с напряженностью электрического поля в виде

Dj = Е×a

с учетом последнего равенства, получаем

Dj = a<v>B

или с учетом (48)

Dj = 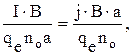(49)

где

R = 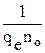- постоянная Холла. (50)

Напряженность поперечного электрического поля (поля Холла) складывается с напряженностью электрического поля, которое обуславливает существование тока в проводнике при отсутствии магнитного поля. Поэтому напряженность электрического поля образует с направлением вектора плотности тока 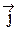некоторый угол, называемый холловским, т. е. напряженность электрического поля Холла

Е = RHjsina,

где Н - напряженность магнитного поля; .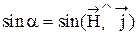

В ферромагнетиках электроны подвергаются совместному действию внешнего магнитного поля и магнитного поля доменов. Это приводит к особому ферромагнитному эффекту Холла, т. е.

Е = (R×H +R_i×J)j,

где R - нормальная постоянная Холла; Н - напряженность внешнего магнитного поля; R_i - аномальная постоянная Холла; J - величина намагниченности домена; j - плотность тока.

Из (50) следует, что знак постоянной Холла R зависит от знака носителя тока. Если R < 0, то проводимость - электронная, если R > 0, то - дырочная. В 1988 г. обнаружен квантовый эффект Холла. Сопротивление Холла зависит от фундаментальных постоянных, и не подвержено влиянию нарушений структуры образца, т. е.

, (51)

где i =1, 2, 3, ... - число состояний; R_H - cопротивление Холла.

Фундаментальные свойства квантового эффекта Холла являются следствием того факта, что энергетический спектр электронов системы состоит из дискретных энергетических уровней. Кроме того, наблюдается дробный эффект квантования холловского сопротивления, из-за частичного заполнения уровней Ландау на 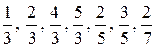при более низких температурах и чистых образцах и вызван взаимодействием электронов двухмерного газа между собой, превращая его в несжимаемую жидкость.