Магнитное поле в веществе. Любое вещество при внесении его во внешнее магнитное поле приобретает магнитный момент, т.е

Любое вещество при внесении его во внешнее магнитное поле 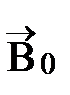приобретает магнитный момент, т.е. намагничивается. Намагниченное вещество создает собственное магнитное поле 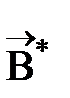. Согласно принципу суперпозиции результирующее магнитное поле

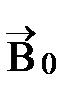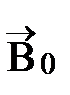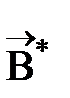= + . (12)

Следовательно, намагничивание вещества обусловлено преимущественной ориентацией магнитных моментов молекул в одном направлении.

Это положение распространяется и на элементарные молекулярные токи (гипотеза Ампера).

Такое поведение молекулярных токов приводит к появлению макроскопических токов I^*, называемых токами намагничивания.

Молекулярные токи в однородном магнетике ориентированы, как показано на рис. 4, а. У соседних молекул молекулярные токи в местах их соприкосновения

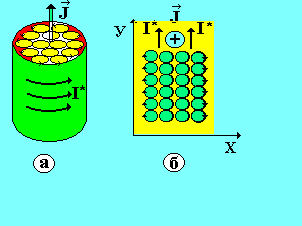Рис. 4

текут в противоположных направлениях и взаимно компенсируют друг друга.

Молекулярные токи, которые выходят на боковую поверхность цилиндрического образца оказываются некомпенсированными и создают поверхностный ток намагничивания I^*.

Внутри неоднородного намагниченного магнетика компенсации молекулярных токов нет, так как сила тока в направлении оси Х возрастает, и возникает объемный ток намагничивания. Вектор 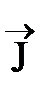направлен за плоскость рисунка (обозначен символом Å) и увеличивается по модулю при возрастании координаты Х (рис. 4, б). Однако распределение токов намагничивания зависит не только от формы и свойств магнетика, но и от искомого поля 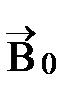. В общем случае задача о нахождении поля 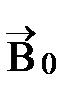в магнетике непосредственно решена быть не может.

Для решения этого вопроса необходимо установить связь между током намагничивания I^* и циркуляцией поля вектора намагничивания .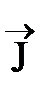

5. Циркуляция вектора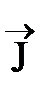

Теорема: В стационарном состоянии циркуляция намагниченности 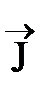по произвольному замкнутому контуру L равна алгебраической сумме токов намагничивания I^*, охватываемых этим контуром, т. е.

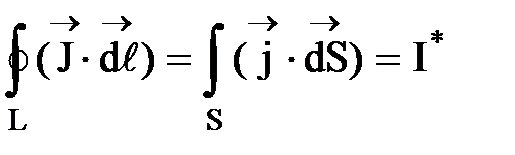. (13)

Натянем на контур L произвольную поверхность S (рис. 5).

Из рисунка видно, что одни молекулярные токи пересекают поверхность S дважды в разных направлениях, поэтому не вносят вклада в результирующий ток намагничивания через эту поверхность.

Другие молекулярные токи пересекают поверхность S только один раз, поэтому и создают макроскопический ток намагничивания, пронизывающий эту поверхность.

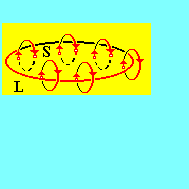Рис. 5

Пусть элементарная площадь S_мол охватывает каждый молекулярный ток I_мол.

Элемент d 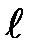контура L (рис. 6) обвивают те молекулярные токи, центры которых попадают внутрь цилиндра с объемом dV= S_молсosa d 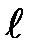, где a - угол между направлением вектора 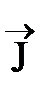и элементом .

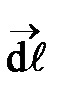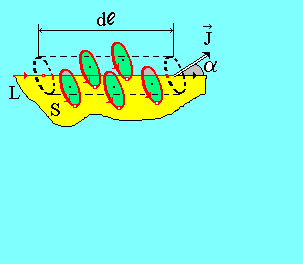Рис. 6

Эти молекулярные токи пересекают поверхность S только один раз и вносят вклад в ток намагничивания

dI^* = I_молndV

или

dI^* = I_молnS_молсosad 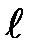= Jсosa = ,

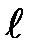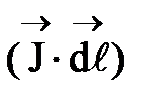где n₀ - концентрация молекул;

р_m = I_молS_мол -

магнитный момент отдельного молекулярного тока; nI_молS_мол - магнитный момент единицы объема вещества.

После интегрирования по всему контуру L последнего выражения, получим формулу (13).

Поле вектора 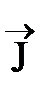зависит от всех токов, как от тока намагничивания I^*, так и от тока проводимости I.

6. Циркуляция вектора

При внесении вещества в магнитное поле возникают токи намагничивания, поэтому циркуляция вектора 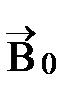будет определяться не только токами проводимости I, но и токами намагничивания I^*, т. е.

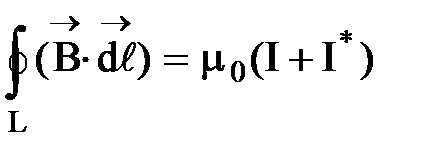. (14)

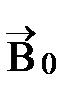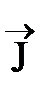Если циркуляция векторов и берется по одному и тому же контуру L, то, решив совместно (13) и (14), получим

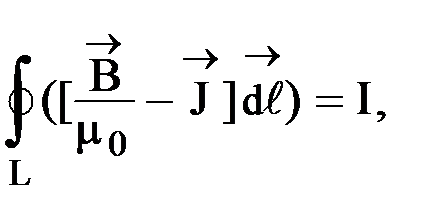(15)

где

(16)

- напряженность магнитного поля.

Следовательно,

. (17)

Эта формула выражает теорему о циркуляции вектора : циркуляция вектора по произвольному контуру L равна алгебраической сумме токов проводимости, охватываемых этим контуром.

Дифференциальная форма теоремы о циркуляции вектора записывается в виде

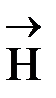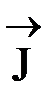[ ´ ] = , (18)

т. е. ротор вектора равен плотности тока проводимости в той же точке вещества. Используя формулы (16), (17) и (18), имеем

(1+c) = .

Так как 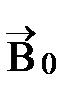= mm₀ , то m = 1 + c. (19)

7. Граничные условия для векторов 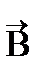и

Найдем условия для векторов 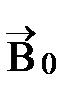и на границе раздела двух однородных магнетиков.

Для нахождения условия для вектора 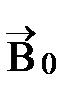применим теорему Гаусса, т. е.

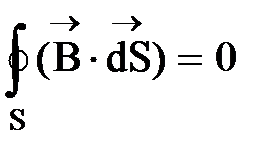. (20)

В качестве замкнутой поверхности возьмем малой высоты цилиндр, расположенный на границе раздела двух магнетиков (рис. 7).

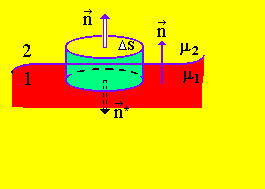Рис. 7.

Полный поток вектора 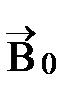сквозь цилиндрическую поверхность запишем с учетом того, что потоком 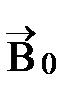сквозь боковую поверхность цилиндра можно пренебречь:

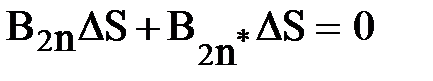. (21)

При нахождении обеих проекций вектора 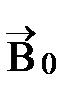на общую нормаль получим 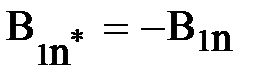и после подстановки в предыдущее равенство получим

. (22)

Следовательно, нормальная составляющая вектора 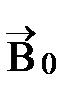одинакова по обе стороны границы раздела магнетиков и скачка не испытывает.

При нахождении условия для вектора используем теорему о циркуляции , формула (17).

Предположим, что вдоль поверхности раздела двух магнетиков течет поверхностный ток проводимости с линейной плотностью i.

В качестве замкнутого контура L используем прямоугольник, высота которого мала по сравнению с его длиной 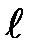(рис. 8).

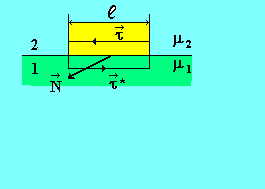Рис. 8

Циркуляция вектора на боковых сторонах контура L практически равна нулю. Поэтому циркуляцию вектора запишем в виде

,

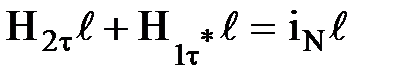где i_N - проекция вектора 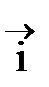на нормаль к контуру (вектор образует с направлением обхода по контуру правовинтовую систему).

Обе проекции вектора возьмем на общий орт касательной 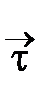(в магнетике 2), т. е.

.

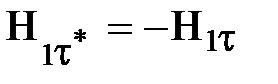С учетом этого предыдущее уравнение принимает вид

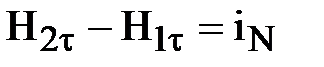. (23)

Вывод: при переходе границы раздела двух магнетиков тангенциальная составляющая вектора испытывает скачок из-за наличия поверхностных токов проводимости.

Если же на границе раздела токов проводимости нет, то тангенциальная составляющая вектора не испытывает скачка, т. е.

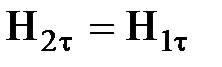. (24)

Таким образом, если на границе раздела двух однородных магнетиков тока проводимости нет, то составляющие В_t и Н_n испытывают скачок. Составляющие В_n и Н_t изменяются н с учетом этого в предыдущем уравнении (24) составляющие Н_2t и Н_1t не испытывают скачка, т. е. изменяются непрерывно.

8. Преломление линий вектора 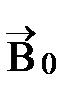и

На границе раздела двух магнетиков с магнитными проницаемостями m₁ и m₂ (m₁ < m₂) линии вектора 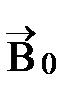испытывают скачок, т. е. преломляются (рис. 9, а, б).

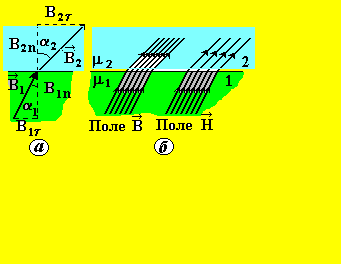Рис. 9

Найдем отношение тангенсов углов a₁ и a₂:

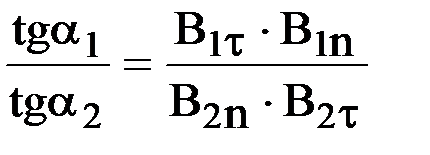. (25)

Если на границе раздела двух магнетиков тока проводимости нет, то

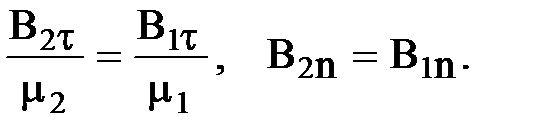(26)

Поэтому закон преломления линий 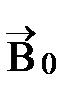и линий запишем в виде

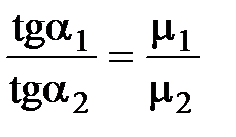. (27)

На явлении преломления силовых линий магнитного поля основана защита приборов от влияния внешних магнитных полей, если их окружить экраном из ферромагнитного вещества, например, железа.