Аппроксимация переходной функции решением дифференциального уравнения с вещественными корнями.

Этот метод применим для аппроксимации гладких кривых переходных функций y(t) неколебательного характера, описываемых уравнением

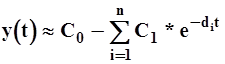(4.16)

где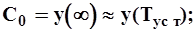

С_i и d_i - вещественные числа, причем корни характеристического уравнения d_i должны удовлетворять эмпирическому неравенству

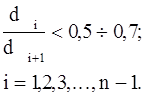(4.17)

Эти условия означают, что аппроксимирующая функция W(P) имеет только вещественные простые полюса, расположенные на достаточно большом расстоянии друг от друга по действительной оси.

Идея метода заключается в последовательном приближении y(t) вначале решением уравнения первого порядка, то есть 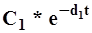; затем, если такая аппроксимация неудовлетворительна, вводится в рассмотрение вторая составляющая 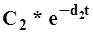, то есть порядок аппроксимирующего уравнения принимается равным двум, и т.д. Неизвестные величины d_i и C_i определяются на каждом этапе аппроксимации с помощью операции логарифмирования, поэтому метод получил название метод последовательного логарифмирования.

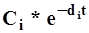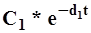
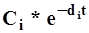Согласно условию (4.17) все корни d_i различны, поэтому скорость убывания функций также будет различной при увеличении аргумента - времени t Скорость убывания определяется величиной d_i и, так как d_i - самый малый из корней, то уменьшается медлене всех прочих составляющих . Поэтому можно предположить, что y(t) есть решение дифференицального уравнения первого порядка, и написать приближенное равенство

y(t) @ C₀- 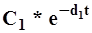(4.18)

или

С₀ - y(t) = y₁(t) @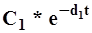

Это соотношение верно при больших значениях времени t, когда влиянием других составляющих 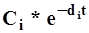можно принебречь.

Прологорифмировав функцию½y₁(t)½, можно получить уравнение прямой линии в полулогарифмическом масштабе по оси ординат:

ln½y₁(t)½ @ lnC₁ - d₁t (4.19)

Отсюда нетрудно определить неизвестные величины d₁ и C₁. Для этого вычисляется функция y₁(t) = C₀ - y(t) и строится график ln½y₁(t)½ в зависимости от времени t. К полученному графику проводится асимптота при больших значениях времени t. Асимптота отсекает на оси ординат некоторый отрезок, равный lnC_1. Величина корня d₁ равна тангенсу угла наклона асимптоты к оси абсцисс:

d_{1 =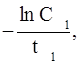} (4.20)

где t₁ - точка пересечения асимптоты с осью времени.

Если y(t) действительно является решением дифференциального уравнения первого порядка, то функция

y₂(t) = y₁(t) - 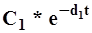(4.21)

равна нулю при всех, а не только при больших значениях времени t, то есть асимптота совпадает со всей функцией ln½y₁(t)½. В общем случае n ¹1; поэтому y₂(t) ¹ 0 при малых значениях t. Зная теперь величины d₁ и C₁ можно найти функцию y₂(t), отражающую неучтенное влияние составляющих 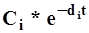и особенно медленно убывающей компоненты .

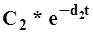Функцию y₂(t) можно построить на графике в полулогарифмическом масштабе по оси ординат, провести к ней асимптоту и определить величины d₂ и С₂. Если асимптота не совпадает со всеми значениями lnïy₂(t)ï, то, очевидно, порядок аппроксимирующего дифференциального уравнения должен быть выше второго. Поэтому следует найти очередную функцию “невязок”

y₃(t) = h₂(t) - 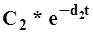(4.22)

и учесть влияние на y(t) следующей составляющей 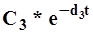и т.д.

Процесс аппроксимации функции y(t) выражением (4.16) прекращается тогда, когда функция y_n(t) » 0 с точностью 1-2% от величины y(T_y), причем значения ее будут знакопеременными. Знаки переменных интегрирования С_i определяются по знакам соответствующих функций y_i(t). Практика показала, что обычно достаточно аппроксимировать функцию суммой двух-четырех экспонент.

4.2. Метод интегральных площадей

Этот метод позволяет по таблично или графически заданной переходной функции y(t) определить коэффициенты a_i, b_i; где i = 1, 2, ..., n и порядок n аппроксимирующей передаточной функции

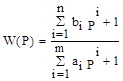(4.23)

Порядок числителя функции всегда меньше или равен порядку знаменателя: n<=m.

Суть метода заключается в разложении функции W^-1(P) в усеченный ряд по степеням P:

W^-1(P) = 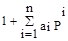(4.24)

и затем определении коэффициентов a₀ и порядка n путем последовательного приближения у(t) решениями линейного дифференциального уравнения первого порядка.

При y(0) = y’(0) = ... = y^(n-1)(0) = 0 можно принять в_{n =} в_n-1 = ... = в1 = 0.

Метод интегральных площадей не связан с графическими построениями и может быть применен при определении динамических характеристик по недостаточно гладким переходным функциям. В этом случае требуется осуществить сглаживание лишь начального и конечного участков y(t), так как именно по ним определяются порядок и коэффициенты передаточной функции W(P).

Метод легко алгоритмизуется и реализуется на ЭВМ. Для невысоких порядков: n<=2¸3 расчет может быть произведен вручную, хотя затраты времени на это в несколько раз больше, чем при использовании метода последовательного логарифмирования.