Аппроксимация переходной функции решением дифференциального уравнения для системы без запаздывания.

При нанесении на вход объекта единичного скачкообразного возмущающего воздействия X(t)=1 получают график переходной функции Y(t)(рис. 5).

Передаточная функция объекта, представляющего собой, например, апериодическое звено I-го порядка, имеет вид:

W(P)=k/(T*P+1) (4.1.)

где T – постоянная времени объекта;

k=y( 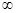) - коэффициент усиления;

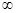y( ) - установившееся значение выходной величины.

Этой передаточной функции соответствует дифференциальное уравнение:

T* 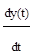+y(t)=k*x(t) (4.2.)

решение которого может быть записано в виде

y(t)=k*x(t)*(1-e 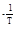) (4.3.)

Постоянная времени Т определяется из графика переходного процесса. Для этого надо провести касательную к кривой y(t) в начале координат; отрезок по оси времени от нуля до точки пересечения касательной и линии y=y( ) равен Т.

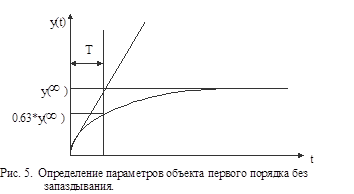
Постоянную времени Т можно определить также, учитывая, что y(T)=0.63*y( ). Для этого по графику переходного процесса находят значение t=T, при котором y(t)=0.63*y( ).

Аппроксимация переходной функции решением дифференциального уравнения для системы с запаздыванием.

Аппроксимирующая передаточная функция для системы первого порядка с запаздыванием имеет вид:

W(P)= 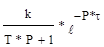(4.4.)

а решение линейного дифференциального уравнения первого порядка с запаздыванием будет

y(t)=0; 0 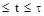(4.5.)

y(t)=k*x(t)*(1- 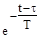); t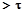

где Т - постоянная времени;

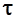- время запаздывания;

К - коэффициент усиления.

Интерполяционный метод определения параметров Т и 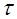заключается в следующем. На нормированной кривой переходного процесса, у которой по оси ординат откладывают величину y(T)/y( 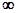), выбирают две точки А и В (рис. 6.)

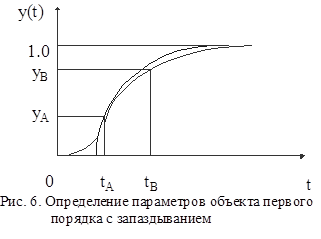
Желательно, чтобы точка А была расположена вблизи точки перегиба кривой, а ордината y(А) равнялась 0.8-0.9. Рассматривая точки А и В как интерполяционные узлы кривой, можно определить параметрами переходной функции:

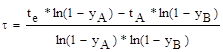(4.6.)

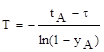(4.7.)

Другой способ аппроксимации переходной функции, являющийся развитием метода Орманна, заключается в следующем. По нормированной кривой y(t) определяется время t₇являющееся корнем уравнения

k*x(t)*(1- 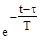)=0.7

и время t 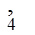, удовлетворяющее равенству y(t 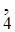)=0.33.

Далее вычисляются время запаздывания :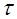

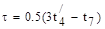(4.8.)

и постоянная времени Т:

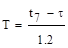(4.9.)

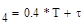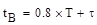
Для проверки полученных результатов сравнивают ординаты заданной переходной функции при t , 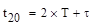с соответствующими значениями ординат аппроксимирующей кривой: h₄ = 0,33; h₈ = 0,55 и h₂₀ = 0,87

Аппроксимация переходной функции решением дифференциального уравнения второго порядка.

Передаточная функция для объекта второго порядка записывается в виде

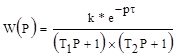(4.10)

Переходная функция объекта может быть аппроксимирована решением линейного дифференциального уравнения второго порядка:

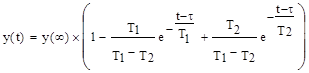(4.11)

Так как время чистого запаздывания t и коэффициент усиления K определяются известными приемами по переходной функции, то далее будем рассматривать только нахождение постоянных времени T₁ и T₂.

Один из способов определения связан с графическими построениями. Исходная переходная функция нормируется путем деления ординат на величину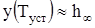

y(t)=y^*(t)/y(T_уст) (4.12)

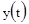- нормированная функция;

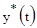- исходная функция;

Т_уст- время, при котором устанавливается постоянное значение .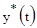

На графике y(t) определяется точка перегиба w , через которую проводится касательная до пересечения с осью абсцисс и горизонтальной прямой y(T_уст) » K (рис. 7).

Точка перегиба кривой y(t) представляет собой точку, в которой производная dy(t)/dt имеет максимальное значение. Так как переходные функции реальных объектов часто не имеют явно выраженной точки перегиба, то определение ее координат можно осуществлять следующим образом.

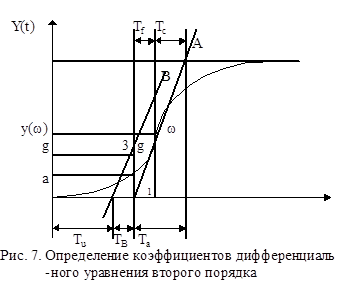
В средней, наиболее быстро изменяющейся части графика y(t) берется несколько ординат y(t_g) = y_g g = 0, 1, 2, ..., q ; q обычно не более 6-7; t_g - t_g-1 = Dt=const и вычисляются первые разности 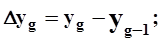g = 0, 1, 2, ..., q-1. Далее находится максимальная величина Dy_g и соответствующее ей значение времени t_w= t_g - 0,5*Dt, а затем ордината y_w.

Из графика y(t) непосредственно находятся значения T₁, T₂ и а. Затем из точки I пересечения касательной А с осью абсцисс восстанавливается перпендикуляр высотой g

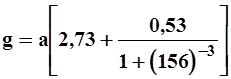(4.13)

Через точку 3 проводится прямая линия B, паралелльная касательной A, и находится время T_в. Предположив, что T₂ < T₁, вычисляют их значения из эмпирических соотношений

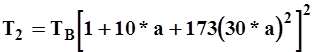(4.14)

при a <= 0,05

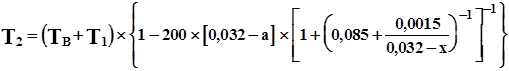(4.15)

T₁= T ₀ - T_в при a > 0,005