Динамических моделей
Обычно при экспериментальных методах построения динамических моделей на вход исследуемой системы подаются испытательные воздействия. Однако во многих случаях другие возмущения, действующие на систему, не удается стабилизировать или хотя бы измерить, а их влияние может существенно исказить результаты эксперимента. Кроме того, для некоторых систем нанесение искусственных возмущений является крайне нежелательным или вообще недопустимым. В этих случаях для построения динамических моделей могут быть использованы статистические характеристики сигналов на входе и выходе системы в процессе ее нормальной эксплуатации.
Задача при этом разбивается на два этапа: определение статических характеристик случайных процессов в системе и затем - построение по ним динамической модели системы.
При исследовании статистических характеристик случайных процессов определяют:
среднее значение случайной величины
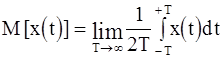(4.26)
корреляционную функцию.
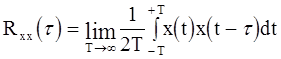(4.27)
взаимокорреляционную функцию
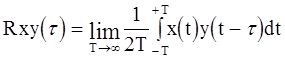
Этот метод позволяет по выборочным реализациям входного и выходного параметров вычислить массив значений импульсной переходной характеристики данного технологического процесса.
Задача формулируется следующим образом: по результатам наблюдений за входными и выходными переменными объекта должна быть построена его модель, оптимальная в смысле минимума средней квадратической ошибки.
Можно предположить, что на входы модели и объекта действует один и тот же сигнал U(t). Разность (x(t)-xм(t)) выходных сигналов объекта x(t) и модели xм(t) поступает на формирователь ошибки, где определяется ошибки идентификации
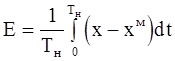(2-32)
где Tн - длительность интервала наблюдения.
Метод идентификации должен минимизировать Е соответствующим подбором импульсной характеристики объекта W(t), т.е.
Е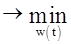 
(2-33)
Вариационная задача определения экстремали W(t) для функционала (2-32) решается различными способами. В описываемом методе импульсная характеристика находится в виде массива значений Wi (i = 1,2,...,m), иначе говоря, в виде решетчатой функции. Такое представление функции удобно для последующих применений. Решетчатые импульсные характеристики позволяют получать простые формулы, связывающие в виде скалярных произведений входные и выходные сигналы объекта. Если необходимо найти аналитическую модель, то от импульсной характеристики легко перейти к переходной и далее по методу Симою - к передаточной функции.
Интеграл свертки связывает входной и выходной сигналы модели:
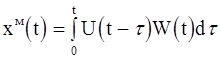(2-34)
Временем памяти объекта T называют время, в течение которого импульсная переходная характеристика уменьшается до малых значений, т.е. принимается
W(t)=0 для t=T (2-35)
С учетом (2-35) формулу (2-34) можно переписать следующим образом:
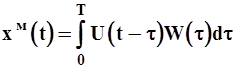(2-36)
Переходя к сигналам, квантованным во времени с интервалом квантования D, запишем интеграл свертки (2-36) в виде суммы
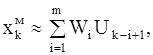(2-37)
где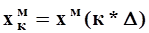 
- текущее значение выходного
сигнала модели на k-м такте;
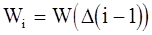- значение i-й ординаты весо-
вой решетчатой функции;
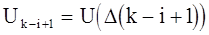- значение выходного сигнала
в (k-i+1) такте;
D - интервал квантования;
m = T/D+1 - число ординат импульсной
характеристики за время
памяти.
Из (2-37) следует, что значение выходного сигнала модели в любом такте k может быть найдено в виде линейной комбинации k-го и (m-1) предыдущих значений входного сигнала. При этом в качестве коэффициентов в сумме (2-37) используются значения импульсной характеристики в точках квантования. Переходя к дискретному времени, (2-32) можно записать в виде:
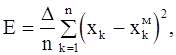(2-38)
где xk = x[D(k-1)] - значение выходного сигнала
объекта на k-м такте;
x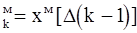 
- значение выходного сигнала
модели на k-м такте;
n = Tн/D+1 - число измеренных значений
выходного сигнала объекта
за интервал наблюдения;
D - интервал квантования.
Из (2-37) видно, что выходной сигнал модели может быть вычислен, начиная с m-го такта, так как для его нахождения требуется m-1 предыдущих значений входного сигнала. Таким образом, начальное значение индекса в сумме (2-38) следует взять равным k=m. Если для идентификации использовать значения выходного сигнала, деленные на интервал квантования D, т.е. xк=x/D, то отыскиваемая модель может быть представлена в виде уравнения линейной регрессии:
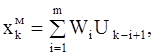(2-39)
параметры которой Wi могут быть найдены методом наименьших квадратов путем минимизации суммы
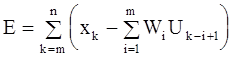(2-40)
Система нормальных уравнений для определения Wi составляется в виде
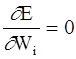(i=1,2,3,...,m) (2-41)
Разделим каждое уравнение (2-41) на n-m и представим в матричной записи полученную систему линейных уравнений:
AW=в (2-42)
где A - квадратная матрица m*m с элементами aij;
W и в - векторы с компонентами Wi и вj.
Элементы матрицы A:
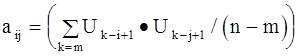(2-43)
(i,j = 1,2,3,...,m)
являются коэффициентами корреляции, сдвинутыми на i-j тактов выборками входного сигнала, поэтому матрица A называется корреляционной.
Если U(t) - стационарный случайный процесс, то строки корреляционной матрицы представляют собой массивы значений оценок корреляционной функции R(i-j). Элементы главной диагонали корреляционной матрицы представляют собой оценки дисперсии входного сигнала. Таким образом, матрица A несет дополнительную информацию и может быть использована для определения статистических характеристик входного сигнала.
Столбец правых членов системы нормальных уравнений имеет вид:
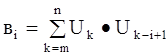(i = 1,2,3,...,n) (2-44)
Для их вычисления требуется m(n-m) умножений.
После решения системы нормальных уравнений и получения оценок значений импульсной характеристики следует провести проверку адекватности полученной модели экспериментальным данным. для этого вычислим отношение
f = SS/SSO (2-45)
где SS =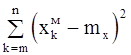 
(2-46)
- остаточная сумма квадратов,
обусловленная регрессией;
SSO =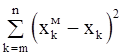 
(2-47)
- остаточная сумма квадратов
относительно регрессии.
Если входной сигнал U(t) представляет собой случайный процесс. то SS и SSO можно рассматривать как случайные величины с m и n-2m-1 степенями свободы соответственно. Их отношение должно подчиняться распределению Фишера. Учитывая, что в реальных задачах идентификации 40>=m>=10 и
n-2m-1>10, можно для проверки адекватности пользоваться верхними точками распределения Фишера F[v1,v2,(1-a)] для v1 и v2>10.
Если f, определенное по формуле (2-45), окажется больше табличного значения, то, приняв модель за адекватную объекту, мы рискуем ошибиться не более, чем в 5% случаев.
При переходе от импульсной к переходной функции пользуются шаговым интегрированием.
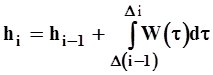(2-48)
i = 2,3,...,m h1 = 0
Интегралы вычисляются по формуле трапеций. При этом (2-48) приобретает следующий вид
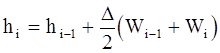(2-49)
i = 2,3,...,m h1 = 0
4.5. Аналитические методы построения
Дата добавления: 2016-01-18; просмотров: 923;