Моделирование процесса тепло- и массообмена в системах с распределенными параметрами
Моделируется процесс тепло- массообмена в слое зерна I, через который продувается сушильный агент 2 (рис. 6.1.).
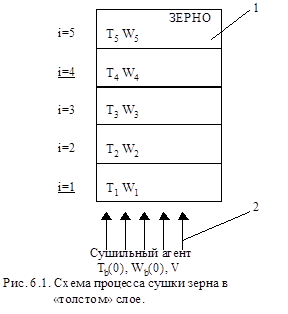
В основе расчета параметров режима сушки зерна в плотном слое лежит упрощенный механизм тепло- и массообмена. в котором приняты следующие предпосылки:
влага в зерне находится в жидком состоянии;
тепло- и массообмен происходит только между сушильным агентом и зерном;
температурный градиент внутри отдельных зерновок пренебрежимо мал;
теплообмен между сушильным агентом и зерном осуществляется путем конвекции.
С учетом сделанных предпосылок процесс сушки можно описать системой дифференциальных уравнений (6-1)-(6-4).
Первое уравнение системы отражает закон сохранения энергии в процессе сушки: тепло, переданное нагретым воздухом (левая часть равенства), расходуется на нагрев зерна и испарение влаги. Второе уравнение составлено в соответствии с законом сохранения вещества.
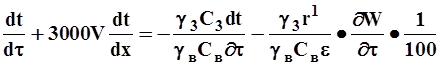 (6-1)
(6-1)
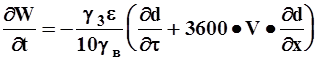 (6-2)
(6-2)
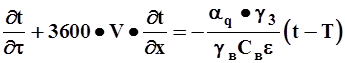 (6-3)
(6-3)
 (6-4)
(6-4)
где t - температура сушильного агента, °С;
d - влагосодержание сушильного агента,
г/кг сухого воздуха;
W - влажность зерна, %;
T - температура зерна, °С;
V - скорость сушильного агента, м/с;
C3, Cв - соответственно теплоемкость зерна и
воздуха, кДж/кг·°С;
e - порозность зернового слоя;
r1 - скрытая теплота парообразования
воды, кДж/кг;
aq - коэффициент теплоотдачи,
ккал/кг·ч·°С;
g3 - объемная масса зерна, кг/м3;
gв - удельный вес воздуха, кг/м3;
K - коэффициент сушки, I/ч;
Wр - равновесная влажность зерна, %;
x - пространственная координата, м;
t - время, ч.
Последние два уравнения отражают соответственно законы тепло- и массообмена между зерном и сушильным агентом.
Решение системы дифференциальных уравнений осуществляется численным методом, основанным на последовательном (во времени и пространстве) расчете процесса сушки тонкого слоя. Изменением влажности и температуры по высоте этого слоя можно принебречь. Процесс сушки тонкого зернового слоя в течение периода времени Dt, за которое скорость сушки изменяется незначительно, описывается системой алгебраических уравнений:
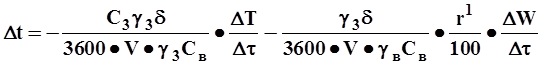 (6-5)
(6-5)
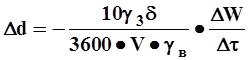 (6-6)
(6-6)
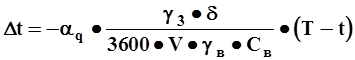 (6-7)
(6-7)
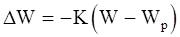 (6-8)
(6-8)
где d - толщина тонкого слоя, м.
Толщину можно определить по формуле
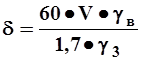 (6-9)
(6-9)
а коэффициент сушки
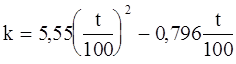 (6-10)
(6-10)
Температура зерна и сушильного агента связаны соотношением
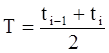 (6-11)
(6-11)
где ti-1, ti - температура сушильного агента соответственно на входе и на выходе i-го слоя °С.
Зависимость (6-11) позволяет исключить из рассмотре-ния уравнения (6-7) и рассчитывать теплообмен в про-цессе сушки по уравнению теплового баланса (6-5).
Таким образом, для i-го тонкого слоя в интервале времени Dt можно будет рассчитать в jDt момент вре-мени значения параметров зерна и сушильного агента:
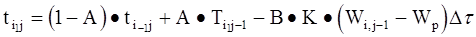 (6-12)
(6-12)
d 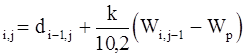 (6-13)
(6-13)
 (6-14)
(6-14)
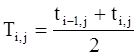 (6-15)
(6-15)
где 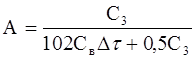 (6-16)
(6-16)
B= 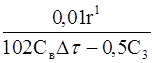 (6-17)
(6-17)
При этом равновесная влажность зерна Wр определяется по формуле Гендерсона:
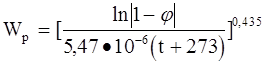 (6-18)
(6-18)
где j - влажность сушильного агента, %
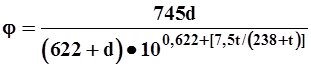 (6-19)
(6-19)
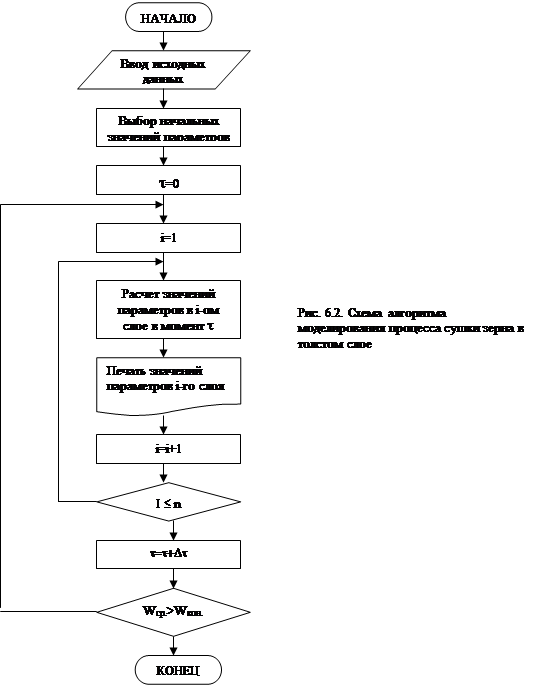
Алгоритм моделирования процесса сушки зерна в толстом слое представлен на рис. 6.2. Алгоритм предусматривает ввод исходных данных (блок 1), установку начальных значений параметров (блоки 2 и 3), циклическое вычисление параметров воздуха и зерна для n слоев зерна и циклическую печать полученных параметров (блоки 4, 5, 6, 7, 8), управление внешним циклом при изменении времени за счет сравнения среднего значения влажности зерна Wср с конечной влажностью Wкон. (блоки 9, 10).
Средняя влажность по всем слоям в каждый момент времени определяется по формуле
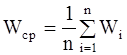 (6-20)
(6-20)
Написав программу для реализации математической модели на ЭВМ, можно провести исследования на модели и определить влияние различных параметров на ход технологического процесса.
Дата добавления: 2016-01-18; просмотров: 1280;
