Вероятностные модели технологических процессов
Стохастическая или вероятностная модель отличается от детермированной тем, что одно или несколько входящих в нее функциональных соотношений зависят от случайных параметров, значения которых подчиняются некоторым распределениям вероятностей. Разработка вероятностной модели сводится к исследованию и анализу случайного процесса, а затем - определению закона распределения вероятностей случайной величины.
При реализации вероятностной модели на ЭВМ необходимо разработать такой генератор случайных чисел, который мог бы генерировать случайные числа с заданным законом распределения. Этот генератор случайных чисел включается в общую схему модели и имитирует влияние случайных факторов на характер протекания технологического процесса.
Рассмотрим некоторые элементы теории вероятностей, необходимые для построения и исследования стохастических моделей.
Вероятность представляет собой количественную меру шансов происшествия или правдоподобного события. Вероятность характеризуется величиной P, определяемой выражением
P = m/n, (4-1)
где m - число интересующих нас событий;
n - общее число рассмотренных событий.
Как можно видеть из неравенства
0<=m<=n (4-2)
значение P заключено между 0 и 1. Вероятность невозможного события равна нулю, а достоверного - единице.
Распределение вероятностей можно представить себе как некоторое систематическое расположение результатов случайных испытаний. Распределение вероятностей выражается в виде функции и иллюстрируется графиком частоты появления случайной величины в различных интервалах.
Изобразим графически результаты какого-либо испытания, например, результаты определения массы молотого кофе в пачках. Значения частоты отложим вдоль оси ординат, а значения измеряемой величины х - вдоль оси абсцисс. Сглаженная кривая этого графика называется функцией плотности вероятности f(x) или плотностью распределения вероятностей случайной величины (рис. 4.1.). Термины “функция плотности” и “плотность распределения” равнозначны. Функция распределения вероятности F(x) является интегралом (или кумулятивной, накопленной величиной) функции плотности вероятности f(x). Кривая функции плотности представляет собой график первой производной функции распределения вероятности, т.е.
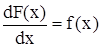 (4-3)
(4-3)
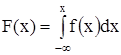 (4-4)
(4-4)

Площадь, находящаяся под кривой функции плотности вероятности всегда равна единице. Площадь, расположенная под частью кривой функции плотности вероятности, равна вероятности P того, что результат случайного измерения xi лежит в интервале между соответствующими значениями абсциссы : x и x+dx, т.е.
P(x < xi < x + dx)
Вид функции распределения вероятностей показан на рис. 4.2. Вероятность того, что случайная величина xi не превышает x, равна значению соответствующей ординаты, т.е.
P(xi < x)
Дата добавления: 2016-01-18; просмотров: 1037;
