Нормальное или гауссово распределение

Нормальное или гауссово распределение является непрерывным, симметричным относительно своего математического ожидания и описывает большинство случайных явлений, связанных и измерениями. Это распределение довольно часто применяется при моделировании на вычислительных машинах.

Биномиальное распределение и распределение Пуассона стремятся к нормальному, когда их математические ожидания стремятся к бесконечности.

Функция одномерного нормального распределения с математическим ожиданием m и дисперсией s² записывается в виде:

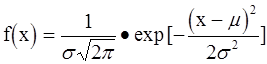(5.25.)

а функция распределения вероятностей F(x) в виде

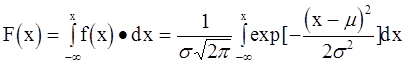(5.26)

Графики этих функций показаны на рис. 12 и 13.

Нормированное нормальное распределение имеет следующие значения четырех моментов: m = 0; s = 1; М₃ = 0; М₄ = 3.

По результатам конечного числа n независимых наблюдений величины m и s² могут быть определены по следующим формулам:

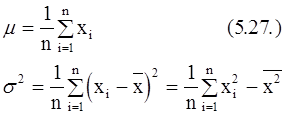(5.28.)

Несмещенная оценка дисперсии случайной величины при выборке равна

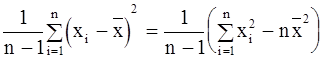(5.29.)

Приблизительное рассеивание случайной величины относительно математического ожидания в единицах s характеризуется для функции нормального распределения следующими интервалами:

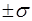содержит не менее 68,3% всех значений

случайной величины;

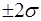содержит не менее 95,5% всех значений

случайной величины;

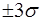содержит не менее 99,7% всех значений

случайной величины.