ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ

Процессы, связанные с массовым обслуживанием, например. прием зерна с водного транспорта в портовый элеватор, зависят от большого количества случайных факторов: количества зерна, времени прибытия судов, качественных показателей зерна, возможных отказов в работе оборудования и др. Такие процессы с большим трудом поддаются анализу традиционными методами и требуют специального подхода к их исследованию.

В подобных обслуживающих системах в случайные моменты времени поступают заявки - требования на выполнение определенной операции обслуживания. Поэтому такие системы называются системами массового обслуживания. Обслуживающая система обычно имеет несколько постов обслуживания, каждый из которых может быть свободен или занят. Если в момент поступления заявки (требования) пост свободен, то обслуживание начинается немедленно. Если свободных постов нет. то в зависимости от типа системы возможно несколько различных подходов к выполнению требования:

система отвечает на требование отказом и в дальнейшем это требование не учитывается (система обслуживания с отказом);

требование ставится в очередь на обслуживание (система обслуживания с ожиданием), причем в некоторых системах, если время ожидания превысит определенное значение, требование аннулируется.

Время выполнения требования постом обслуживания (время обслуживания) является случайной величиной. При анализе систем массового обслуживания необходимо учитывать возможность случайных выходов из строя обслуживающих аппаратов и случайное время, необходимое для их восстановления. Работа всей системы может прерываться по причине выхода из строя оборудования; при этом образуются очереди требований. Если очередь переполнена, то последующие требования стираются, а система, после восстановления ее работоспособности, постепенно “рассасывает” оставшуюся очередь. Каждая обслуженная системой заявка поступает на склад обслуженных требований.

При массовом обслуживании соблюдается определенная дисциплина очереди, например, требование ожидает до тех пор, пока его не начнут обслуживать, и соответствующий порядок обслуживания, например: “первый пришел - первый ушел” или “первым пришел - последним ушел” или различные виды приоритетов.

В теории массового обслуживания обычно рассматриваются “простейшие” (пуассоновские) потоки требований, которые характеризуются следующими свойствами:

вероятность появления требования не зависит от принятого начала отсчета времени, а зависит только от продолжительности периода наблюдения (свойство стационарности);

вероятность поступления требования в интервале времени (t, t + t) не зависит от того, какое число требований имело место до момента времени t (отсутствие последствия);

в каждый момент времени может поступать только одно требование (ординарность потока требований).

Для простейшего потока требований вероятность поступления точно K требований на протяжении интервала времени t определяется законом распределения Пуассона:

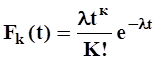(6.1.)

где l - параметр потока, равный математическому

ожиданию числа требований, поступающих

в систему в единицу времени.

В случае простейшего потока требований случайные величины интервалов между поступлениями требований 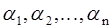взаимно независимы. а их функция плотности имеет вид:

x > 0 (6.2.)

Анализ системы массового обслуживания должен установить количественные характеристики работы системы, определяющие качество обслуживания. Типичными являются следующие характеристики системы обслуживания:

количество требований в единицу времени, поступающих в систему, на каждый пост обслуживания, на каждый аппарат;

производительность всей системы, каждого поста обслуживания, каждого аппарата; время и причины простоев;

продолжительность рассасывания очереди требований в системе, в том числе по каждому отдельному аппарату, линии;

функции распределения требований, поступающих на вход системы и на каждый отдельный аппарат.

Из-за сложности процессов массового обслуживания возможности их исследования аналитическими методами весьма ограничены. Однако для этой цели могут быть эффективно использованы ЭВМ, позволяющие на основе метода случайных испытаний производить моделирование работы системы массового обслуживания. Такое моделирование состоит в многократном воспроизведении при помощи соответствующего алгоритма моделируемого процесса обслуживания и статистической обработке получаемых результатов для установления характеристик исследуемой системы.

В данной работе в качестве примера имитационного моделирования рассматривается исследование изменения массы муки в приемном бункере хлебобулочного комбината.

Мука поступает на предприятие в автомуковозах 1 (рис. 7.1.) и подается пневмотранспортером 2 в бункер 3, где хранится в течение какого-то промежутка времени. Из бункера мука небольшими партиями с помощью пневмотранспортера 4 отпускается на производство.

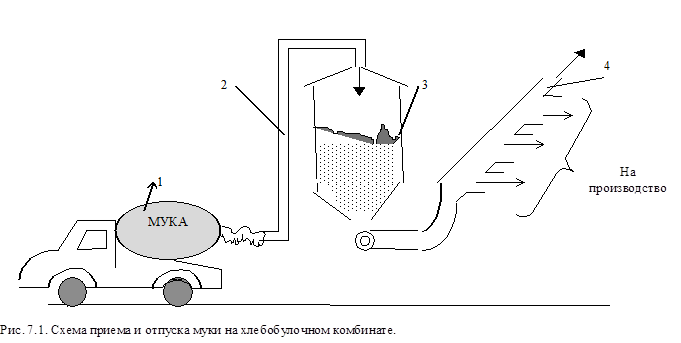
Промежуток времени между двумя последовательными прибытиями автомуковозов принимается равным t₁; масса муки, которую доставляет на предприятие каждый муковоз составляет Q₁; масса партии муки, единовременно отпускаемой на производство, принимается равной Q₂; промежуток времени между двумя последовательными отпусками муки составляет t₂. Все перечисленные величины являются случайными. Предполагается, что они распределены по нормальному закону. Параметры нормального закона распределения вероятностей m и s для каждой случайной величины известны: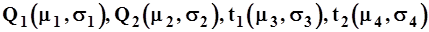

Предполагается также, что за достаточно длительный промежуток времени среднее количество муки, пребывающее на предприятие в единицу времени, равно среднему количеству муки, отпускаемому в единицу времени на производство, т.е.

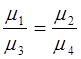(7-1)

Необходимо, используя метод имитационного моделирования, определить:

минимальное начальное количество муки М_min в бункере, которое гарантировало бы беспребойный отпуск муки на производство;

максимальную массу муки М_max, которую должен вместить бункер, чтобы избежать простоев автомуковозов при их прибытии.

Модель имитирует процессы поступления муки, ее хранения и отпуска на производство.

Схема моделирующего алгоритма представлена на рис. 7.2.

Алгоритм предусматривает ввод исходных данных в ЭВМ (блок 1) и генерацию начальных значений случайных величин: Q₁, T₁, Q₂, T₂. При этом в начальный момент времени t = 0 масса муки в бункере также принимается равной нулю (блок 2). В зависимости от того, какое событие произойдет раньше: прием или отпуск муки, блок 3 осуществляет переключение в программе. Затем моделируется процесс приема муки и генерируются новые данные по заявке на прием муки (блоки 4, 5) или моделируется процесс отпуска муки и генерируется новая заявка на отпуск муки (блоки 6, 7). В том и другом случаях определяется величина шага моделирования Dt, равная t₁ или t₂ в зависимости от того, какой процесс произошел: приема или отпуска муки. Затем из всех предшествующих значений массы муки в бункере определяются максимальное и минимальные значения (блок 8). В следующем блоке определяется текущее значение времени и, если оно не превышает времени окончания моделирования, то цикл повторяется (блок 10). В противном случае печатаются результаты моделирования (блок 11), и машинный эксперимент заканчивается.

Поскольку полученные значения М_min и М_max являются результатами машинного эксперимента и тоже носят случайный характер, необходимо провести ряд дополнительных экспериментов, например, за несколько месяцев, по которым определить средние значения и средние квадратические отклонения этих величин. Кроме того, следует определить доверительный интервал оценки дисперсии с заданной доверительной вероятностью P.

При конечном числе степеней свободы полученная при анализе результатов машинного эксперимента оценка дисперсии является смещенной и ее доверительный интервал не будет симметричен относительно этой оценки

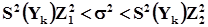(7-2)

где s - истинное значение среднего квадратического отклонения;

Z₁, Z₂ - коэффициенты, значения которых берут из таблицы 7.1 в зависимости от принятого уровня значимости a и числа степеней свободы f (Z₂>Z₁).

Таблица 7.1

Значения коэффициентов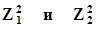

a	Z2	Число степеней свободы f
0,05		0,20	0,27	0,32	0,35	0,39	0,48	0,54	0,58	0,63
0,05		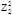	39,5	13,9	8,26	6,02	3,08	2,40	2,08	1,79
0,01		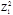0,12	0,18	0,28	0,26	0,29	0,39	0,45	0,50	0,55
0,01		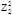		41,8	19,3	12,1	4,64	3,26	2,69	2,18

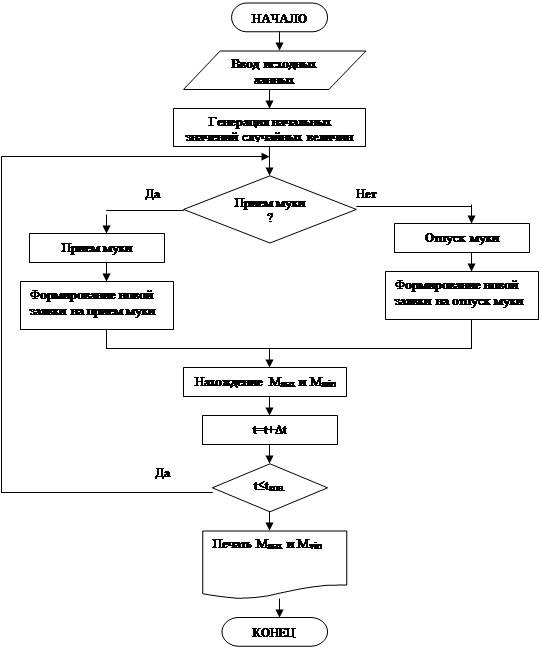
Рис. 7.2. Схема алгоритма имитационного моделирования