Биномиальному закону

Для получения случайных чисел, распределенных по биномиальному закону, необходимо предварительно сформировать последовательность n равномерно распределенных случайных чисел, где n выбирается небольшим. Случайная биномиальная величина равняется количеству равномерно распределенных случайных чисел, не превосходящих по величине P.

Рассмотрим пример получения случайной биномиальной величины описанным выше способом. Найдем ее для биномиального распределения, у которого n = 7 и P = 0,3. Выберем семь равномерно распределенных случайных чисел: 0,02011; 0,85393; 0.97265; 0,6168; 0,16656; 0,42751; 0,69994. Как видно два из них не превышают по величине 0,3. Следовательно, случайная биноминальная величина равна 2.

При больших значениях n и малых P биномиальную величину можно получить следующим образом. Возьмем случайное число U и будем повторять операцию суммирования до тех пор, пока не удовлетворится неравенство

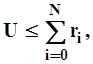(5.44.)

где r₀ = (1-P)ⁿ (5.45.)

r_i+1 = r_i 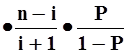(5.46.)

Случайная биномиальная величина S равняется числу итераций N, которые нужно выполнить, чтобы удовлетворилось неравенство (5.44.).

Проверка случайности последовательности М чисел S_i, полученных для заданных значений n и P, производится следующим образом. Вычисляют математическое ожидание и дисперсию для полученной последовательности чисел и, если выполняются условия:

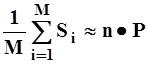(5.47.)

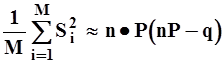(5.48.)

где q = 1 - P,

то эти числа являются случайными и удовлетворяют заданному закону распределения.