Распределение Стьюдента или t - распределение
Это распределение является производным от одномерного нормального. Оно имеет симметричную функцию плотности вероятности, среднее значение которой совпадает с началом координат. Функция плотности f(t) с r степенями свободы имеет вид:
f(t) =  (5.34.)
(5.34.)
Математическое ожидание и дисперсия соответственно равны:
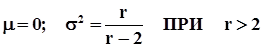
Распределение Стьюдента используется в t - критерии для проверки гипотезы о том, что две независимые выборки принадлежат совокупности с одним и тем же средним значением.
F - распределение
Это распределение является непрерывным, связанным с одномерным нормальным и имеет функцию плотности f(x), определенную для неограниченных и только положительных значений аргумента.
 (5.35.)
(5.35.)
Математическое ожидание и дисперсия для F - распределения соответственно равны:
m= 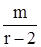 (5.36.)
(5.36.)
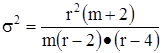 (5.37.)
(5.37.)
где m и r - числа степеней свободы, вычисленные
для двух выборок.
F - распределение используется при проверке гипотезы о принадлежности двух выборок генеральным совокупностям с одной и той же дисперсией.
Определение закона распределения
Случайных чисел
Для определения закона распределения случайных чисел берут выборку из n независимых наблюдений и определяют диапазон изменения случайной величины x. Весь диапазон делят на разряды одинаковой ширины, но так, чтобы значение частоты в каждом разряде было не меньше 5. Обычно ширину разряда выбирают такой, чтобы на одно стандартное отклонение приходилось не менее 2,5 разрядов.
Затем определяют абсолютную (Wi) и относительную (fi) частоту появления случайной величины в каждом разряде. Относительная частота fi определяется как Wi/n. После этого строят гистограмму распределения случайной величины в координатах fi и x (рис. 4.7.)
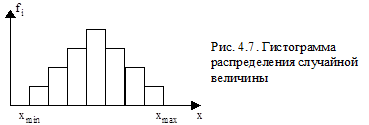
По внешнему виду гистограммы предпологают, что случайная величина х распределена по тому или иному закону.
Проверка гипотезы о соответствии распределения выбранному закону поводится с помощью критерия x2. Для этого определяется расчетное значение критерия
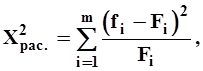 (4-21)
(4-21)
где fi - экспериментальное значение относительной частоты, взятое из гистограммы;
Fi - теоретическое значение частоты, соответствующее среднему значению x в i-ом разряде для предполагаемого закона распределения;
m - количество разрядов.
Значение x 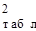 берется из таблицы 4.1. Если выполняется условие
берется из таблицы 4.1. Если выполняется условие 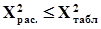 , то гипотеза о соответствии распределения выбранному закону принимается на уровне значимости a.
, то гипотеза о соответствии распределения выбранному закону принимается на уровне значимости a.
Таблица 4.1.
Процентные точки распределения x2
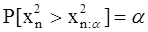
| a | n | ||||||||||||
| 0,05 | 3,84 | 5,99 | 7,81 | 9,43 | 11,07 | 18,31 | 25,0 | 31,41 | 37,65 | 43,77 | 55,76 | 79,08 | |
| 0,01 | 6,63 | 9,21 | 11,34 | 13,28 | 15,09 | 23,21 | 30,58 | 37,57 | 44,31 | 50,89 | 63,09 | 88,38 |
n - число уровней свободы; a - уровень значимости.
Число степеней свободы определяется
n = m -3 (4-22)
После того, как определен закон распределения случайной величины, можно говорить о том, что имеется модель изменения случайной величины. Для реализации этой модели на ЭВМ необходимо построить генератор случайных чисел (ГСЧ), который будет генерировать на выходе случайные числа с заданным законом распределения. На базе ГСЧ с заданными параметрами может быть построена вероятностная модель технологического процесса.
5.2. Генерирование случайных чисел
Дата добавления: 2016-01-18; просмотров: 1158;
