Равномерно распределенные случайные числа

Равномерно распределенные случайные числа могут выбираться из таблиц или генерироваться с помощью вычислительной подпрограммы. Эти случайные числа заключены в интервале от нуля до единицы и выбираются случайным образом в соответствии с функцией равномерного распределения

F(x) = x, 0 <= x <=1

При этом распределении одинаково правдоподобно появление любых значений случайной величины в интервале (0,1).

Способы генерирования, основанные на многократном повторении некоторой операции, используют фактически искусственный путь для получения случайных чисел. Поэтому полученные таким образом последовательности случайных чисел называют “псевдослучайными равномерными последовательностями”.

Один из наиболее простых способов получения псевдослучайных равномерных чисел - способ средних квадратов - разработан фон Нейманом и состоит в том, что исходное случайное число возводится в квадрат. В качестве следующего случайного числа берется последовательность цифр, стоящих (по нумерации разрядов) на среднем месте в вычисленном квадрате. Эта последовательность цифр содержит столько же разрядов, сколько и исходное число. Затем полученное число используют путем возведения в квадрат для нахождения нового случайного числа, и таким образом процесс повторяется.

Другой метод заключается в реализации следующего алгоритма:

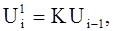(5.38.)

где K = 8t ± 3

t - целое число; U₀ - нечетное число;

Ui - равномерно распределенные числа,

представляющие собой последнюю

значащую чисел U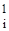

Для проверки равномерности распределения N случайных чисел U_i вычисляют их математическое ожидание и дисперсию. Случайные величины считаются распределенными равномерно, если

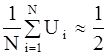(5.39.)

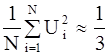(5.40.)