Экспоненциальное распределение. Это непрерывное распределение, график функции плотности которого представляет собой экспоненциальную функцию с началом в точке x = 0

Это непрерывное распределение, график функции плотности которого представляет собой экспоненциальную функцию с началом в точке x = 0. В качестве примеров экспоненциального распределения можно привести следующие: срок службы электронных приборов, интервалы времени между последовательными отказами электронных приборов, испытания на долговечность, модели отказов, разрыв электрических цепей, неисправности сложных механизмов.

Экспоненциальное распределение представляет собой распределение Пирсона X-типа. Функция плотности распределения его равна:

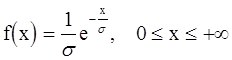(5.31.)

а функция распределения вероятностей задается в виде:

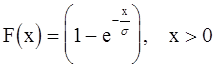(5.32.)

Математическое ожидание и дисперсия для экспоненциального закона распределения соответственно равны: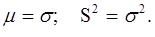

Вид функции плотности распределения вероятностей для экспоненциального закона показан на рис. 14.

Распределение c²

Распределение c² является непрерывным и связано с одномерным нормальным распределением. Функция плотности вероятности f(c²) c r степенями свободы равна

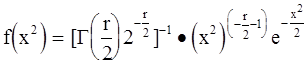(5.33.)

где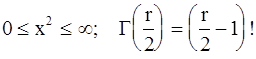

График функции плотности вероятности имеет колоколообразную форму (рис. 15).

Математическое ожидание и дисперсия для распределения соответственно равны: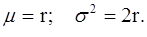

Функции Х² необходимы при использовании критерия для проверки согласия статистических данных.