Распределение Пуассона

Пуассоновское распределение представляет собой дискретное распределение, описывающее редкие случайные события. Пуассоновскому распределению подчиняются, например, количество дефектов в готовом изделии; количество аварий в единицу времени; число вызовов, поступающих на телефонный коммутатор в единицу времени; потребность в причалах судов в порту; поступление заказов в торговую точку.

Пуассоновское распределение является предельным для биномиального. Если предположить, что в биномиальном распределении при очень большом числе независимых испытаний n стремится к бесконечности, а P - к нулю, причем произведение n·P остается постоянным, то получаем

, (5.15.)

характеризующее распределение Пуассона.

Для данных n и P вероятность того, что все исходы будут неблагоприятны, можно определить с помощью функции

(5.16.)

где nP - среднее количество или математическое

ожидание благоприятных исходов.

Вероятность одного или более благоприятных исходов определяется следующим образом:

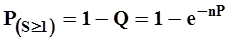(5.17.)

Вероятность точно одного и точно двух благоприятных исходов равна соответственно

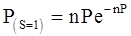(5.18.)

(5.19.)

Биномиально распределение (распределение Бернулли)

Это распределение является дискретным и предполагает для случайного события только два возможных исхода - благоприятный и неблагоприятный.

Вероятность того, что в n реализациях некоторого эксперимента будет получено S благоприятных исходов равна

(5.11.)

где P - вероятность благоприятного исхода.

Функция распределения записывается в виде:

(5.12.)

K = 0,1,2,...,n

Для биномиального распределения математическое ожидание и дисперсия соответственно равны

m = n · P (5.13.)

s² = n · P(1-P) = n · P · q, (5.14.)

где q = 1 - P - вероятность неблагоприятного исхода.