T – критерий Стьюдента
Критерий применяется в случае, когда стоит задача сравнить средние показатели двух распределений.
Критерий основан на оценке общих частей двух распределений.
Ограничение критерия состоит в том, что распределения должны быть нормальными.
Эмпирическое значение критерия вычисляется по формуле:
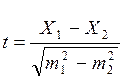
| 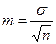 - ошибка средней, Х1 и Х2 средние арифметические двух сравниваемых распределений; n – объем соответствующей выборки. - ошибка средней, Х1 и Х2 средние арифметические двух сравниваемых распределений; n – объем соответствующей выборки.
|
Эмпирическое значение критерия сравнивается с критическими для f степеней свободы по таблице 7 приложения 2, где 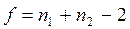 .
.
Пример. В 10 и 8 классе предлагался невербальный тест структуры интеллекта Кеттелла. В таблице 33 представлены результаты суммы баллов по 4 субтестам. Различаются ли средние показатели в данных классах?
Решение:
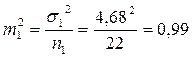 ;
; 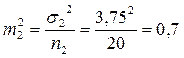
Таблица 33
Обобщенный показатель теста Кеттелла
учащихся 10 и 8 классов
| 10 класс | 8 класс | ||||||
| № исп. | Балл | № исп. | Балл | № исп. | Балл | № исп. | Балл |
| Х | 29,09 | Х | 27,25 | ||||
| s | 4,68 | s | 3,75 |
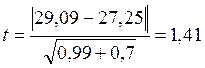
f=22+20-2=40. Для f=40 – t0,01=2,704, t0,05=2,021
tэмп < t0,05, следовательно, экспериментальная гипотеза отвергается.
Ответ: 10 и 8 класс по средним показателям невербального интеллекта, измеренного по тесту Кеттелла, не различаются.
Дата добавления: 2016-01-26; просмотров: 1433;
