Частотный метод построения динамических моделей
В соответствии с этим методом параметры передаточной функции или коэффициенты дифференциального уравнения определяют исходя из экспериментально полученной амплитудно-фазовой характеристики исследуемой системы.
Амплитудно-фазовая характеристика линейной системы с сосредоточенными параметрами записывается в виде
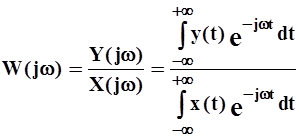
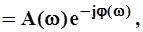(4.25)
где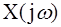 
и 
- преобразованные по Фурье
соответственно входная x(t) и выходная y(t) переменные;
A(w) - амплитудно-частотная характеристика;
j(w) - фазо-частотная характеристика.
Амплитудно-частотная характеристика показывает степень усиления или ослабления системой гармонических колебаний, подаваемых на ее вход. Фазо-частотная характеристика отражает величину сдвига фаз между входными и выходными гармоническими колебаниями системы. При экспериментальном определении частотных характеристик искусственным путем возбуждаются гармонические колебания входной переменной x(t) с частотой w и регистрируются установившиеся колебания выходной величины Y(t). Измерения проводятся при различных значениях частоты w. Для нахождения A(w) измеряются амплитуды x(t) и y(t) и берется их отношение; для определения j(w) - временные сдвиги между гармониками входных и выходных колебаний.
Результаты эксперимента обрабатываются на ЭВМ с получением коэффициентов дифференциального уравнения, описывающего динамику исследуемой системы.
Частотные характеристики относятся к числу наиболее удобных описаний динамики технологических процессов. Для экспериментального снятия частотных характеристик существует достаточно совершенная аппаратура. Входной параметр процесса изменяют с заданной частотой и амплитудой. После затухания переходного процесса измеряют характеристики изменения выходного параметра: амплитуду колебаний A и фазовый сдвиг j между входной и выходной гармониками или вещественную Re и мнимую Im составляющие частотной характеристики.
Таким образом, экспериментальные частотные характеристики представляют собой совокупность точек, которые определяются тремя координатами:
в прямоугольной системе координат w, Re(w), Im(w)
в полярной системе координат w, А(w), j(w).
Предлагаемый метод [4] может быть использован для обработки экспериментальных частотных характеристик обоих видов.
Задаются m строк по 3 столбца. Вид координат определяет заданная переменная vid.
Описываемый метод позволяет производить идентификацию как объектов и систем с самовыравниванием, так и объектов с интегрирующими звеньями, количество которых не более двух. Таким образом, принята аппроксимация передаточной функции в виде
(2-14)
При этом n<=5, а int может принимать одно из трех значений: 0, 1 или 2. Это число задается среди исходных данных. Определение коэффициентов k и ai осуществляется методом наименьших квадратов.
Рассмотрим инверсную передаточную функцию (предположив вначале, что int = 0)
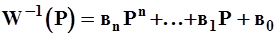(2-15)
где 
Вычисление параметров в0,...,вn представляет собой теперь линейную задачу оценки коэффициентов полинома. Определив в0,..., вn, легко можно найти
Подставляя в (2-15) вместо P=jw, выделяя в полученном выражении действительную и мнимую части и учитывая, что n<=5, запишем:
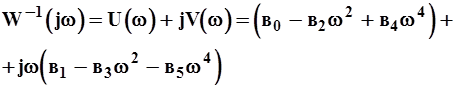(2.16)
Из (2-16) можно получить два уравнения, приравнивая соответственно мнимые и действительные части.
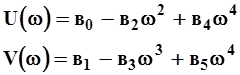(2.17)
Левые части уравнений могут быть найдены из экспериментальных данных. В правых частях вi - искомые параметры, а w - экспериментальные величины.
Таким образом, вычислительная задача сводится к простейшему регрессивному анализу, на основании которого определяются коэффициенты в0, в2, в4 из первой регрессии и в1, в3, в5 из второй.
Запишем выражения для U(w) и V(w) через экспериментальные величины. Если vid=1, т.е. дана прямоугольная система координат, то
откуда
(2.18)
Если частотная характеристика задана в полярных координатах, т.е. vid=0, то
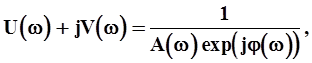
откуда
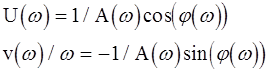(2-19)
Это для случая int=0. Для других случаев приведем без вывода: vid=1 int=1
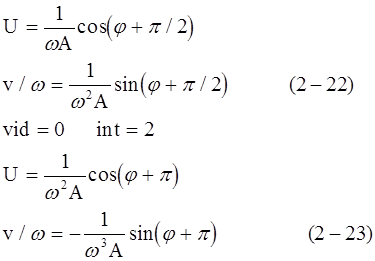
Уравнение регрессии (2-17) сходны между собой. Их можно записать в общем виде:
(2-24)
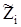- определяется через экспериментальные значения wi и неизвестные коэффициенты Cj.
Коэффициенты Cj по методу наименьших квадратов находятся минимизацией суммы квадратов отклонений:
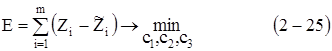
где Zi - экспериментальная величина.
Если в качестве Zi используются значения Ui, то искомые коэффициенты соответствуют:
в0 = С1
в2 = -С2
в4 = С3 (2-26)
Если в качестве Zi используются значения Vi/w, то получаем:
в1 = С1
в3 = -С2
в5 = С2
Система нормальных уравнений для отыскания коэффициентов Cj имеет вид:
Подставляя сюда сумму квадратов отклонений (2-25) и учитывая уравнение регрессии (2-17), можно получить:
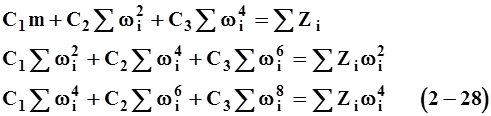
Здесь и далее в этом алгоритме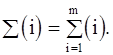 
Если задан порядок аппроксимации n = 5, то для отыскания коэффициентов в0,...,в5 необходимо решить две системы нормальных уравнений вида (2-28), отличающихся столбцами правых частей. Положив Zi = Ui и решая систему (2-28), находим С1, С2, С3, а затем из (2-26) в0, в2, в4. Положив затем Zi = vi/w и решая систему (2-28), находим C1, С2, С3, а затем из (2-27) - в1, в3, в5.
Если n = 4, то для коэффициентов в0, в2, в4 решается система (2-28) при Zi = Ui, а для отыскания в1, в3 нужно решить систему их двух линейных уравнений:
При этом Zi = Vi/wi. Коэффициенты в1 и в3 находятся через С1 и С2 согласно (2-27). Если n = 3, то решаются две системы из двух уравнений (2-29). Если n = 2, то решается одна система (2-29) и уравнение
где С1 = в1.
При n = 1 решаются два уравнения вида (2-30), из которых определяются:
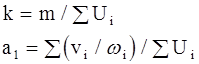(2-31)
4.4. Статистический метод построения
Дата добавления: 2016-01-18; просмотров: 846;