ДИНАМИЧЕСКИЕ МОДЕЛИ

Динамическая модель описывает зависимость между входными и выходными параметрами процесса при изменении их во времени. Она может быть представлена в виде передаточных функций или в виде дифференциальных уравнений.

В зависимости от того, каким образом получают исходные данные для построения динамической модели, используют тот или иной метод обработки экспериментальных данных. Наиболее распространенными являются метод построения динамической модели по графику переходного процесса, частотный метод и статистический метод.

Для экспериментального определения параметров динамической модели используют переходные функции, полученные при скачкообразном внешнем возмущении, частотные характеристики объектов или результаты статистического анализа. В зависимости от реальных возможностей наносить те или иные возмущения системе и от требований, предъявляемых к точности математической модели, выбирается тот или иной метод построения динамической модели.

Дифференциальное уравнение в общем виде запишется так:

A_n*Y⁽ⁿ⁾(t)+A_n-1*Y^(n-1)(t)+...+A₁*Y^I(t)+A₀*Y(t) = B_mX^(m)(t)+B_m-1X^(m-1)(t)+...+B₁*X^I(t)+B₀*X(t)

Для решения дифференциального уравнения используются операционные исчисления, для чего все функции действительной переменной “t” преобразуются в функцию комплексной переменной 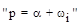. Используя преобразования Лапласа получим:

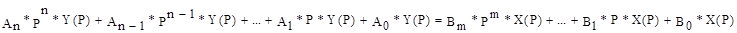
Передаточная функция - это отношение изображенного по Лапласу выходного сигнала элемента к вызвавшему его входному сигналу.

W(P)=Y(P)/X(P)

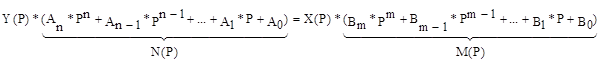
W(P)=M(P)/N(P)