Контур с током в неоднородном магнитном поле

Рассмотрим плоский контур с током в неоднородном магнитном поле (рис. 35). Пусть (для простоты) контур имеет форму окружности. Предположим также, что магнитная индукция увеличивается в положительном направлении оси х, совпадающем с направлением вектора магнитной индукции 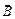. Сила Ампера 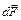, действующая на элемент контура 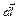, перпендикулярна к вектору 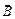(рис. 35, а). Так что силы, приложенные к различным элементам контура, образуют симметричный конический «веер» (рис. 35, б, в).

Если магнитный момент контура 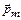ориентирован по полю ( 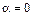) (рис. 35, б), то результирующая всех сил 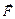направлена в сторону увеличения густоты линий магнитной индукции, т. е. контур будет втягиваться в область более сильного поля. Втягивание будет тем сильнее, чем больше модуль градиента поля 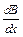. Докажем это утверждение.

С учетом (2.23) элементарная работа сил поля

.

Следовательно,

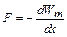. (2.24)

Для контура малых размеров, когда магнитную индукцию в точках плоскости, ограниченной контуром, можно считать одинаковой, согласно (2.21) в случае 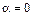имеем выражение

после подстановки его в (2.24) получаем

,

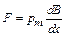что и требовалось доказать: сила пропорциональна градиенту магнитной индукции.

В случае, когда магнитный момент контура 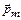ориентирован в направлении, противоположном полю ( 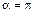) (рис. 34, в), контур будет выталкиваться в область более слабого поля.

В общем случае неоднородного поля, когда 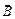не перпендикулярен плоскости контура ( ), на контур с током будут действовать пара сил, стремящихся повернуть контур, и сила, приводящая к его поступательному движению. Величина последней будет зависеть не только от градиента поля, но и от ориентации контура в пространстве.

Когда 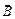зависит только от одной координаты, подстановка (2.21) в (2.24) дает величину силы, обусловливающей поступательное перемещение контура:

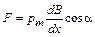. (2.25)

В общем случае неоднородного поля, когда 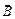есть функция всех координат, сила, действующая на контур с током, определяется выражением

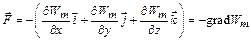. (2.26)

Подставив выражение (2.21) в (2.26), получаем выражение для силы, действующей на малый по размерам контур с током:

. (2.27)

Соотношение (2.27) показывает, что действие магнитного поля на контур с током зависит от магнитной индукции, от свойств контура ( 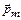) и от его ориентации в пространстве ( ).

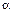2.6. Работа, совершаемая при перемещении проводника с током
в магнитном поле. Магнитный поток

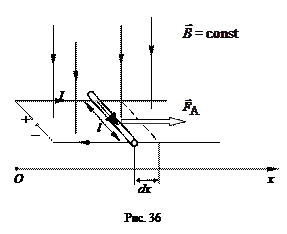
Рассмотрим простейшую замкнутую цепь, изображенную на рис. 36, в которой наряду с источником постоянного тока имеется прямолинейный проводник, который может свободно перемещаться в горизонтальной плоскости. Проводник находится в хорошем электрическом контакте с другими проводниками цепи. Пусть I – сила тока в цепи, магнитное поле однородно, а вектор магнитной индукции 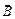перпендикулярен к плоскости проводящего

контура. Для указанных на рисунке направлений тока и поля на подвижный проводник длиной l будет действовать сила Ампера 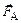, направленная вправо вдоль оси OX. Согласно (2.13)

.

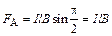Для элементарной работы силы Ампера 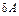справедливо выражение

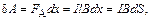(2.28)

где dx – элементарное перемещение подвижного проводника вдоль оси OX, а dS = l dx – площадь, пересекаемая проводником с током при его движении.

Полученный результат (2.28) легко обобщить на случай неоднородного поля и проводника произвольной формы. Для этого нужно разбить проводник на отдельные участки 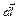и сложить элементарные работы, совершаемые при перемещении каждого из них (рис. 37). В пределах малой площадки dS магнитную индукцию B можно считать постоянной. Найдем работу, совершаемую при произвольном бесконечно малом перемещении элемента тока 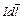вдоль оси ОХ (рис. 37). Пусть элемент тока переместился на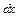 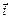, где 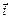– единичный вектор направления ОХ. При этом сила Ампера совершит работу:

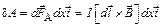. (2.29)

Осуществив в (2.29) циклическую перестановку сомножителей, получим

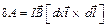. (2.30)

Векторное произведение 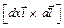равно по модулю площади параллелограмма, построенного на векторах 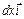и :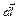

,

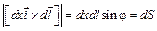т. е. площади, пересекаемой элементом тока при его перемещении. Направление векторного произведения по правилу правого винта совпадает с направлением нормали к площадке dS (рис. 37). Таким образом, (2.30) можно записать в виде

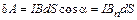, (2.31)

где 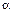– угол между вектором магнитной индукции 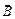и вектором нормали 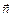к поверхности dS; 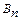– проекция вектора магнитной индукции на направление нормали к поверхности dS.

Полученный результат (2.31) можно представить в более удобном виде, если ввести понятие потока вектора магнитной индукции (магнитного потока) аналогично тому, как вводилось понятие потока вектора напряженности в электростатике [3]. В общем случае неоднородного магнитного поля произвольную поверхность S можно разбить на бесконечно малые элементы dS (рис. 38). Каждый элемент поверхности можно рассматривать как плоскую площадку, а поле в пределах ее – как однородное. Пусть 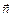– единичный вектор нормали к площадке dS. Для потока вектора магнитной индукции через элемент поверхности dS справедливо выражение

d ,

а для потока через всю рассматриваемую поверхность –

.

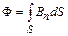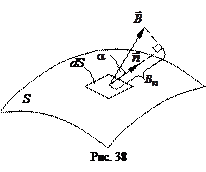Заметим, что поток вектора 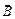–величина алгебраическая, знак которой зависит от знака проекции 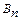, который, в свою очередь, зависит от выбора направления нормали 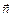. Принято связывать направление нормали с направлением тока в проводящем контуре правилом правого винта (подразд. 1.1).

Введение понятия потока позволяет переписать выражение (2.31) для элементарной работы в виде

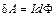. (2.32)

Если контур с постоянным током совершает конечное перемещение, то

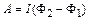, (2.33)

где 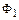и 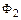– потоки магнитной индукции, сцепленные с контуром в начале и в конце его перемещения соответственно.

Если контур состоит из N последовательно соединенных одинаковых витков, то вводится величина

,

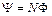которая называется потокосцеплением или полным потоком магнитной индукции. В этом случае выражение (2.33) для работы, совершаемой силами магнитного поля по перемещению контура с током, имеет вид

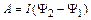. (2.34)

В заключение отметим, что работа силы Ампера во всех рассмотренных выше случаях совершается не за счет энергии магнитного поля, а за счет энергии источника, поддерживающего ток в контуре постоянным. Далее в курсе общей физики будет показано, что любое изменение магнитного потока, сцепленного с проводящим контуром, сопровождается возникновением в нем эдс индукции:

.

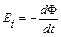При этом источник совершает дополнительную работу против эдс индукции, определяемую выражением

,

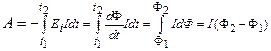что совпадает с (2.33).