в последовательном колебательном контуре
Изучение вынужденных колебаний
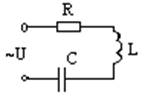 Рисунок 1
Рисунок 1
|
Принципиальная схема последователь-ного колебательного контура изображена на рисунке 1. Чтобы в контуре совершались вынужденные колебания, необходимо включить последовательно с элементами контура переменную ЭДС, создающую на контактах разрыва цепи переменное напряжение
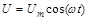 .
.
Уравнение колебательного контура для вынужденных колебаний имеет вид
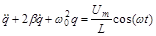 ,
,
где собственная частота колебаний контура  и коэффициент затуха-ния
и коэффициент затуха-ния 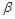 определяются по формулам
определяются по формулам
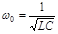 и
и 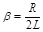 .
.
При установившихся вынужденных колебаниях изменение величины заряда на обкладках конденсатора описывается уравнением
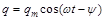 ,
,
где
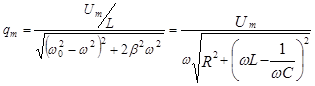 ;
;
 .
.
Сила тока в контуре при установившихся колебаниях изменяется по закону
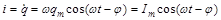 ,
,
где 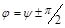 - сдвиг по фазе между током в контуре и приложен-ным напряжением
- сдвиг по фазе между током в контуре и приложен-ным напряжением 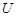 . Значения
. Значения 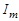 и
и 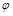 определяется из формул
определяется из формул
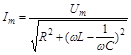 (1)
(1)
и 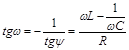 . (2)
. (2)
Можно считать, что сумма падений напряжения в колебательном контуре равна напряжению, приложенному извне
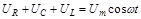 ,
,
где напряжения на каждом из элементов контура равны
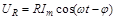 ,
,
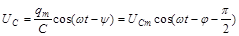 ,
,
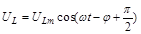 .
.
Значения 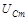 и
и 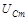 связаны с
связаны с 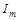 соотношениями
соотношениями
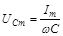 и
и  .
.
Фазовые соотношения между 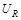 ,
, 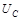 и
и 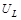 можно представить с помощью векторной диаграммы, показанной на рисунке 2. Напряжение на ёмкости отстаёт по фазе от тока на
можно представить с помощью векторной диаграммы, показанной на рисунке 2. Напряжение на ёмкости отстаёт по фазе от тока на 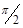 , а на индуктивности опережает ток на
, а на индуктивности опережает ток на 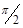 .
.
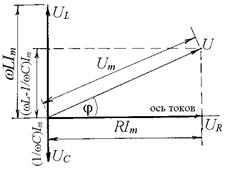 Рисунок 2
Рисунок 2
|
Напряжение на активном сопротивлении изменяется в фазе с током. При 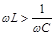 приложенное к контуру нап-ряжение
приложенное к контуру нап-ряжение 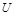 опережает ток по фазе и
опережает ток по фазе и 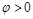 (в соответствии с формулой (2)); при
(в соответствии с формулой (2)); при 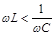 ток будет опере-жать напряжение и
ток будет опере-жать напряжение и 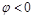 . При
. При 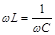 ток в контуре будет определяться значением активного сопротивления
ток в контуре будет определяться значением активного сопротивления 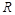 и будет максимальным:
и будет максимальным:
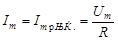 .
.
Это явление называется резонансом напряжений, так как при этом напряжение на конденсаторе 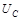 в каждый момент времени будет равно по величине напряжению на индуктивности
в каждый момент времени будет равно по величине напряжению на индуктивности 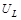 , но противоположно ему по фазе. Резонансная частота для тока в контуре
, но противоположно ему по фазе. Резонансная частота для тока в контуре 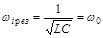 , т.е. резонансная частота для тока равна собственной частоте контура.
, т.е. резонансная частота для тока равна собственной частоте контура.
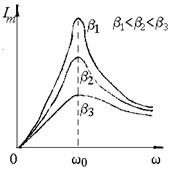 Рисунок 3
Рисунок 3
|
Кривая зависимости амплитуды си-лы тока в контуре 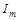 от частоты внешнего источника
от частоты внешнего источника 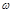 (формула (1)) называется резонансной кривой для тока. Вид этой кривой для различных значений коэффициента затухания
(формула (1)) называется резонансной кривой для тока. Вид этой кривой для различных значений коэффициента затухания 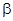 показан на рисунке 3, из которого вид-но, максимум при резонансе тем выше и острее, чем меньше активное сопро-тивление
показан на рисунке 3, из которого вид-но, максимум при резонансе тем выше и острее, чем меньше активное сопро-тивление 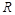 и больше индуктивность L. При
и больше индуктивность L. При 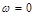 ток I = 0, т. е. при пос-тоянном напряжении установившийся ток в цепи с конденсатором проходить не может.
ток I = 0, т. е. при пос-тоянном напряжении установившийся ток в цепи с конденсатором проходить не может.
Амплитудное значение напряжения на конденсаторе 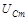 также за-висит от частоты
также за-висит от частоты 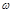 внешнего источника ЭДС. При этом максимальное значение Ucm достигается при частоте
внешнего источника ЭДС. При этом максимальное значение Ucm достигается при частоте
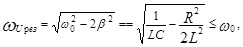
называемой резонансной частотой для напряжения, которая в реальном контуре меньше собственной частоты контура w0 .
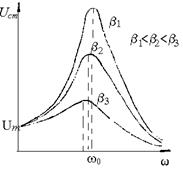 Рисунок 4
Рисунок 4
|
Вид резонансных кривых для напря-жения на конденсаторе показан на рисунке 4 для различных b. При w®0 резонансные кривые сходятся в одной точке с ординатой Ucm=Um равной напряжению на конденсаторе при подключении его к источнику постоянного напряжения Um.
Широко используемой характе-ристикой колебательного контура является его добротность Q. Это безразмерная величина, характери-зующая относительную величину по-терь энергии в контуре: 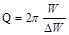 , где DW - потеря энергии за один период и W - энергия в контуре в данный момент. Добротность связана с логарифмическим декрементом затухания l и числом колебаний Ne, совершаемых за промежуток времени, в течение которого амплитуда уменьшается в e раз, соотношением
, где DW - потеря энергии за один период и W - энергия в контуре в данный момент. Добротность связана с логарифмическим декрементом затухания l и числом колебаний Ne, совершаемых за промежуток времени, в течение которого амплитуда уменьшается в e раз, соотношением
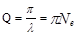 .
.
При малом затухании (b2 <<  )
)
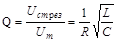 .
.
Таким образом, добротность контура показывает, во сколько раз напряжение на конденсаторе контура может превышать приложенное напряжение.
Добротность контура определяет также остроту резонансных кривых. На рисунке 5 показана ширина резонансной кривой Dw для амплитуды тока, равной 0,7Imрез, что соответствует 0,72 » 0,5 мощности при резонансе. Можно показать, что при малом затухании
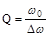 , (3)
, (3)
т.е. чем меньше ширина резонансной кривой, тем выше добротность.
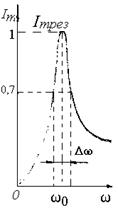 Рисунок 5
Рисунок 5
|
4 ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ
1 Звуковой генератор.
2 Электронный осциллограф.
3 Переменный резистор.
4 Катушка индуктивности.
5 СХЕМА ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
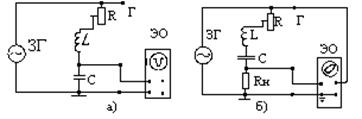 Рисунок 6
Рисунок 6
|
Для изучения вынужденных колебаний в контуре используется установка, изображенная на рисунке 6, а). С помощью этой установки можно изучать зависимость амплитудного напряжения на конденсаторе Ucm от частоты w внешнего источника эдс. При этом на вход Y осциллографа подается напряжение с конденсатора С. В качестве внешнего источника переменного напряжения используется звуковой генератор ЗГ. Активное сопротивление контура можно менять с помощью переменного резистора R.
6 ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1 Включить осциллограф и звуковой генератор в сеть и дать им про-греться 5...7 минут.
2 Установить на выходе генератора напряжение до 3 В.
3 Усиление осциллографа и его временную развертку установить так, чтобы на экране наблюдалось около 10 периодов колебаний.
Меняя частоту генератора wi и усиление на входе Y осциллографа добиваемся того, чтобы при резонансе (максимальная амплитуда Uсmрез) сигнал не выходил за рамки экранной сетки. Сопротивление контура должно быть при этом минимальным.
Снять зависимость амплитуды напряжения Uсmi (в делениях экранной сетки) и осциллографа) от частоты wi (всего 8...10 измерений). Резонансные значения должны находиться примерно посередине диапазона измерений. Зависимость Uсmi(wi) снять Повторить измерения, указанные в пунктах 3-4, для 3-4 разных значений сопротив-ления Ri. Результаты измерений занести в таблицу 1.
6 Не меняя усиления входа Y осциллографа, подать на этот вход вместо исследуемого напряжения Ucm напряжение непосредственно со звуко-вого генератора (клемма Г). Определить амплитудное значение напряжения генератора Um (также в делениях сетки экрана). Напряжение Um должно слабо зависеть от R, поэтому можно ограничиться измерением этого напряжения только для одного значения активного сопротивления.
Измерить напряжение, подаваемое от звукового генератора Um . Для этого напряжение с клеммы Г подать на вход вольтметра, отсоединив от него конденсатор (рис. 6а).
Таблица 1
| R(Ом) | 5(резонанс) | |||||||||
| R1 | wi | |||||||||
| Ucmi | ||||||||||
| R2 | wi | |||||||||
| Ucmi | ||||||||||
| R3 | wi | |||||||||
| Ucmi | ||||||||||
| R4 | wi | |||||||||
| Ucmi |
7 ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
1 По данным таблицы 1 построить резонансные кривые UÑm=U(w) для различных R.
2 По результатам графического измерения ширины резонансных кри-вых Dw определить добротность контура для разных R по формуле (3). Результаты занести в таблицу 2. Построить график зависимости Q=Q(R).
Таблица 2
| С о п р о т и в л е н и е | ||||
| Добротность | R1 | R2 | R3 | R4 |
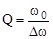
| ||||
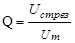
|
3 Определить добротность контура 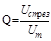 для разных R. Результаты занести в таблицу 2. Нанести полученные точки на график Q = Q(R) и сравнить полученные результаты.
для разных R. Результаты занести в таблицу 2. Нанести полученные точки на график Q = Q(R) и сравнить полученные результаты.
8 ДОПОЛНИТЕЛЬНОЕ ЗАДАНИЕ
Определить сдвиг фаз между током в цепи и приложенным напря-жением в зависимости от частоты внешней эдс, т.е. снять фазовую ха-рактеристику колебательного контура j = j(w).
Для снятия фазовой характеристики контура используется та же экспериментальная установка, что и при выполнении основного зада-ния. С помощью переключателя можно перейти от схемы, показанной на рисунке 6а), к схеме на рисунке 6б). При этом на вход Y осциллографа подается напряжение, пропорциональное току в контуре, а на вход X - напряжение звукового гене-ратора.
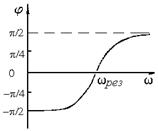 Рисунок 7
Рисунок 7
|
Подобрав соответствующее усиле-ние по каналам X и Y, получим на экране эллипс, являющийся результатом сложения двух взаимно перпендикулярных колебаний. Ориентация эллипса относительно координатных осей зависит от угла сдвига фаз j (формула (2)), который, в свою очередь, зависит от частоты w. Измеряя полуоси эллипса a и b, можно определить сдвиг фаз j:
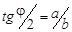 и
и 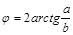 .
.
В задании необходимо определить сдвиг фаз для различных значе-ний частоты внешней ЭДС. Для этого, изменяя частоту генератора w вблизи резонансной частоты (резонанс соответствует вырождению эл-липса в прямую), измерить полуоси эллипса на экране и занести данные в таблицу 3. Опыт проделать для 2...3 значений R.
Таблица 3
| R1 | R2 | ||||||
| w | a, мм | b, мм | j | w | a, мм | b, мм | j |
По данным таблицы 3 построить фазочастотные характеристики j=j(w). Примерный вид фазочастотной характеристики показан на рисунке 7.
| <== предыдущая лекция | | | следующая лекция ==> |
| С ПОМОЩЬЮ ФИГУР ЛИССАЖУ | | | исследование разряда конденсатора и определение его емкости |
Дата добавления: 2016-01-03; просмотров: 2472;
