С ПОМОЩЬЮ ФИГУР ЛИССАЖУ

ГРАДУИРОВКА ЗВУКОВОГО ГЕНЕРАТОРА

Для определения частоты неизвестного гармонического колебания часто используется метод фигур Лиссажу, который заключается в следующем. Неизвестное исследуемое синусоидальное колебание складывают с взаимно перпендикулярным ему синусоидальным колебанием известной частоты, в результате чего получаются кривые сложной формы, называемые фигурами Лиссажу, по общему виду которых можно определить частоту неизвестного колебания и в некоторых случаях разность фаз.

Рассмотрим два взаимно перпендикулярных колебания Х и У с частотами w_х = w и w_y = n×w. Тогда

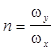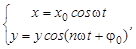, и (1)

где х₀, у₀ - амплитудные значения Х и У;

j₀ - начальная разность фаз между колебаниями;

n - номер гармоники.

Система уравнений (1) представляет собой уравнение плоской кривой, являющейся результатом сложения двух взаимно перпендикулярных гармонических колебаний, заданной в параметрической форме.

Определим уравнение этой кривой в явном виде, исключая из системы уравнений (1) время. Несложные математические преобразования приводят к уравнению вида (2).

Разлагая правую часть уравнения (2) по биному Ньютона и приравнивая действительные части слева и справа, получаем уравнение кривой в явном виде, являющейся траекторией колеблющейся точки. Эта кривая называется фигурой Лиссажу.

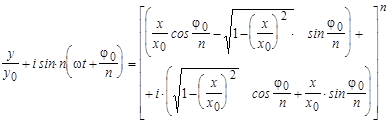(2)

Пример. Рассмотрим сложение колебаний с одинаковыми частотами (n = 1). Тогда уравнение (2) примет вид

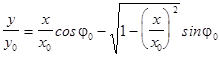, (3)

откуда

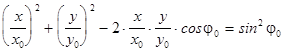. (4)

Уравнение (4) является уравнением эллипса. Рассмотрим частные случаи этого уравнения.

1. Колебания Х и У происходят в одинаковых фазах, т.е. Y₀=0 ® j₀ = 0. Тогда уравнение (4) примет вид

,

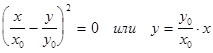т.е. эллипс вырождается в прямую (рис.1).

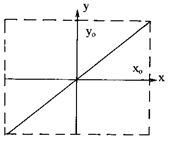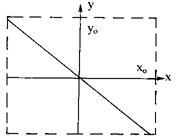Рисунок 1 Рисунок 2

2. При разности фаз j₀ = p уравнение (4) станет уравнением прямой (рисунок 2)

.

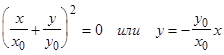3. При j₀ = p/2 получим уравнение эллипса (рис.3)

.

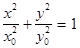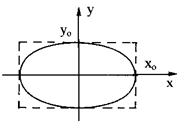
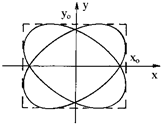
Рисунок 3 Рисунок 4

4. В случае произвольных значений j₀ фигура Лиссажу будет иметь вид эллипса, как показано на рис. 4.

Таким образом, при n = 1 суммарное колебание происходит в общем случае по эллипсу. Вид эллипса определяется разностью начальных фаз j₀.

Более сложные кривые получаются при неравных частотах (n ¹ 1). Если 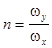не является рациональным числом, то кривая будет незамкнутой (неповторяющейся) и с течением времени заполнит весь прямоугольник со сторонами 2х₀ и 2y₀.

Если n - рациональное число, т.е. 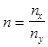, где n_x и n_y - целые числа, то уравнение (2) будет определять различные кривые, вид которых зависит от значения n и разности начальных фаз j₀. Вид различных фаз показан на рис. 5.

,

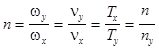где w_x, n_x,T_x и w_y, n_y, T_y - cоответственно частоты и периоды колебаний в направлениях Х и У. Тогда n_yT_x=n_xT_y=Dt, где Dt₁ - промежуток времени, за который точка совершит n_x полных колебаний в направлении оси Y и n_y полных колебаний в направлении оси Х. За следующий промежуток времени Dt = Dt₁ колебания в точности повторяются.

В результате колебания будут накладываться друг на друга и дадут замкнутую устойчивую фигуру Лиссажу.

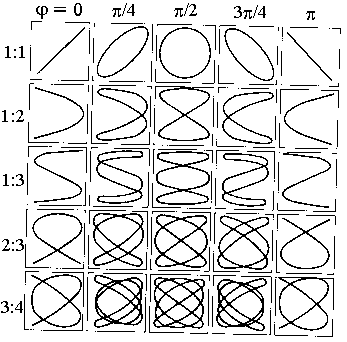Рисунок 5

4 ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ

1 Электронный осциллограф.

2 Звуковой генератор.

3 Лабораторный автотрансформатор с вольтметром (ЛАТР).

5 ОПИСАНИЕ УСТАНОВКИ

В настоящей работе сравнение частот производится с помощью электронного осциллографа.

Для этого на У-вход осциллографа подается синусоидальное напряжение от звукового генератора, а на Х-вход - синусоидальное напряжение с частотой w = 2pn (n = 50 Гц) от клеммы «контрольный сигнал» на осциллографе. (Синусоидальное напряжение с n = 50 Гц можно подавать на Х-вход от сети переменного тока через ЛАТР).

В результате сложения двух взаимно перпендикулярных напряжений с частотами 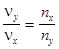, где n_x и n_y - целые числа, на осциллографе получится замкнутая устойчивая кривая (фигура Лиссажу). Тогда

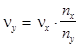. (5)

Для определения отношения 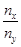рекомендуется использовать следующее правило. Проводятся взаимно перпендикулярные координатные оси Х и У через полученную фигуру Лиссажу. Подсчитываем число точек пересечения кривой с осью Х (n_x) и с осью У (n_y).

В случае, когда ось проходит через точку пересечения ветвей кривой (точка А, рис. 7), при подсчете ее считают дважды. Для фигуры Лиссажу, изображенной на рис. 7: n_x = 3; n_y = 4, т.е.

.

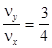6 ХОД РАБОТЫ

1. Собрать схему в соответствии с рисунком 6.

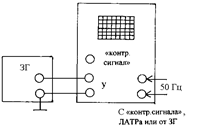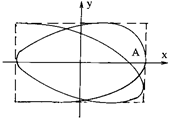Рисунок 6 Рисунок 7

2. Выключить генератор развертки осциллографа (рукоятка «диапазон частот» в положение «выкл.») и устанавливают рукоятки усиления по осям Х и У на ноль. Рукоятка ЗГ «амплитуда» также устанавливается на ноль.

3.Включить в цепь звуковой генератор, осциллограф и ЛАТР (ЛАТР включается в цепь, если у осциллографа нет «Контрольного сигнала»).

4. Сфокусировать световое пятно на экране осциллографа.

5. Увеличивая амплитуду сигнала от звукового генератора и меняя его частоту (поворотом лимба генератора), получить ряд фигур Лиссажу и по их форме определить частоту сигнала звукового генератора при данном положении его лимба.

6. Зарисовать наблюдаемые фигуры Лиссажу как показано на рис. 5 и записать в таблицу найденную частоту и показания лимба ЗГ.

7. Построить градуировочный график, откладывая по оси абсцисс деления ЗГ, а по оси ординат соответствующие частоты.