Классификация магнетиков. Магнитные свойства атомов

Магнетики – так называются вещества в магнетизме. Это связано с тем, что все без исключения вещества в той или иной степени влияют на магнитное поле, ослабляя или усиливая его.

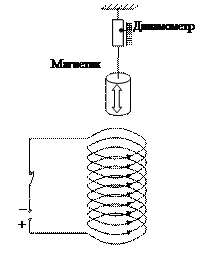
На рис. 39 представлена схема опыта по изучению действия магнитного поля на различные вещества [7]. Сравнение показаний динамометра до и после включения постоянного тока в соленоиде указывает на три возможных типа взаимодействия.

Первый тип взаимодействия: относительно слабое втягивание магнетика в область более сильного поля. Такие вещества называются парамагнетиками. К парамагнетикам относятся, например, алюминий, платина, натрий, хлористая медь, жидкий кислород и др.

Второй тип взаимодействия: относительно слабое выталкивание магнетика в область менее интенсивного поля. Эти вещества называются диамагнетиками. К ним относятся медь, серебро, висмут, углерод, вода, жидкий азот и др.

Третий тип взаимодействия: для веществ этого класса наблюдалось втягивание в область более сильного поля, и их можно было бы, формально, отнести к первому типу взаимодействия. Однако эффект в тысячи, десятки тысяч раз превосходит силы, наблюдавшиеся для парамагнетиков и диамагнетиков. Эти вещества называются ферромагнетиками. К ним относятся, например, железо, кобальт, никель и др.

Почему же вещества по-разному взаимодействуют с магнитным полем? Естественно предположить, что то или иное взаимодействие магнетиков с магнитным полем обусловлено магнитными свойствами атомов. Еще в начале XIX столетия Ампер выдвинул гипотезу молекулярных токов, согласно которой каждому атому (молекуле) можно сопоставить некоторый круговой ток с соответствующим магнитным моментом. В современной физике магнитный момент атома рассматривается как суммарный магнитный момент, связанный с орбитальным движением электронов вокруг ядра, собственным магнитным моментом электронов и с магнитным моментом ядра:

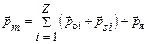, (3.1)

где Z – число электронов в атоме; 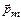– суммарный магнитный момент атома; 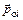– орбитальный магнитный момент i-го электрона, обусловленный движением электрона вокруг ядра; 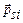– собственный магнитный момент i-го электрона; 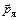– суммарный магнитный момент ядра, обусловленный магнитными моментами входящих в состав ядра протонов и нейтронов.

Как показывает опыт, магнитный момент ядра мал по своей величине, и им можно пренебречь по сравнению с магнитными моментами электронов, считая, что магнитный момент атома равен векторной сумме орбитальных и собственных магнитных моментов электронов.

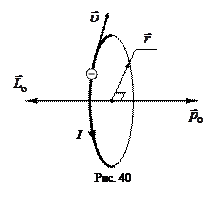
Рассмотрим движение электрона по круговой орбите радиуса 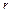вокруг ядра как круговой контур с током (рис. 40). Если электрон за одну секунду делает 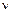оборотов, то сила тока в таком контуре

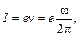
где 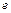– модуль заряда электрона; 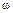– циклическая частота. Тогда для орбитального магнитного момента такого контура площадью 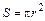получаем

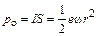. (3.2)

Направление тока I противоположно скорости электрона 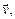так как заряд электрона – отрицательный (рис. 40).

Здесь уместно ввести понятие гиромагнитного отношения 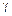– отношения орбитального магнитного момента электрона 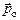к его орбитальному моменту импульса :

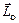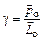. (3.3)

Момент импульса (момент количества движения) был определен в разделе «Механика» [6]:

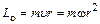, (3.4)

где m – масса электрона. Вектор 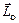направлен противоположно вектору 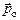(рис. 40).

Как видно из (3.2)–(3.4), связь между векторам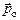и и 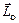можно выразить в виде

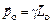, (3.5)

где гиромагнитное отношение для орбитального движения электрона

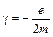. (3.6)

Из (3.6) следует, что гиромагнитное отношение не зависит от параметров орбитального движения электрона и для всех электронов одинаково.

Электрон обладает также собственным магнитным моментом 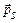и собственным моментом импульса 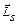. Последний называют также спином. Соответственно собственный магнитный момент называют спиновым магнитным моментом. Собственные моменты электрона имеют квантовую природу и являются такими же неотъемлемыми его характеристиками, как масса и заряд. Опыт показывает, что собственный магнитный и механический моменты электрона связаны соотношением

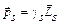, (3.7)

где 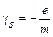– гиромагнитное отношение для этих моментов. Рассмотренные ранее орбитальные моменты могут различаться для разных электронов атома. В отличие от них величины собственных магнитных моментов 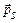одинаковы у всех электронов, это же справедливо и для собственных механических моментов 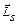. Например, они одинаковы у свободного и у связанного в атоме электронов.

В атоме (молекуле) векторная сумма орбитальных и собственных магнитных моментов электронов равна полному магнитному моменту атома (молекулы). Вследствие этого атомы (молекулы) можно рассматривать как микроскопические круговые контура с током, получившие в физике название молекулярных токов Ампера.

Как показывает опыт, для парамагнетиков и ферромагнетиков суммарный магнитный момент атомов (молекул) отличен от нуля. Для диамагнетиков при отсутствии магнитного поля он равен нулю. Явления парамагнетизма, диамагнетизма и ферромагнетизма будут рассмотрены соответственно в подразд. 3.2, 3.3 и 3.5.

Парамагнетики

Итак, магнитные моменты атомов парамагнетика не равны нулю. В отсутствие магнитного поля тепловое движение атомов магнетика приводит к тому, что ориентация их магнитных моментов носит случайный характер. Если парамагнетик поместить в магнитное поле с индукцией 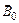, то на каждый атом парамагнетика, как на рамку с током в магнитном поле (подразд. 2.4), будет действовать момент сил, стремящийся повернуть частицу так, чтобы ее магнитный момент 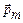был направлен вдоль линий магнитной 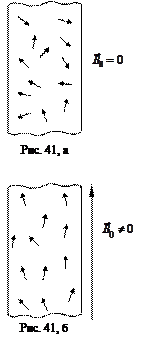индукции. Совместное действие поля и теплового движения атомов приведет к появлению преимущественной ориентации магнитных моментов атомов вдоль линий магнитной индукции. Для наглядности на рис. 41 маленькие стрелки представляют ориентацию магнитных моментов атомов парамагнетика при выключенном (рис. 41, а) и включенном (рис. 41, б) магнитном поле. Для характеристики влияния магнитного поля на магнетик вводится вектор намагничивания (намагниченность) 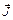, равный магнитному моменту единицы объема магнетика:

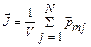, (3.8)

где 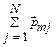– векторная сумма магнитных моментов атомов в физически малом объеме 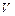с числом атомов N. Напомним, что под физически малым объемом понимается объем, с одной стороны, содержащий достаточно большое 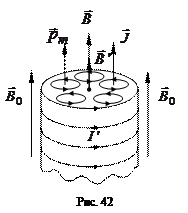количество молекул, чтобы можно было проводить статистическое усреднение. С другой стороны, объем настолько мал, что концентрацию молекул в его пределах можно считать одинаковой, а магнитное поле – однородным.

Докажем, что парамагнетики усиливают магнитное поле. Рассмотрим некоторый парамагнетик, имеющий форму цилиндра и помещенный в однородное магнитное поле параллельно линиям магнитной индукции. На рис. 42 схематично показаны молекулярные токи Ампера в одном из сечений намагниченного парамагнетика. Токи Ампера в объеме парамагнетика компенсируются противоположно направленными соседними токами Ампера. Поэтому эти токи не создают макроскопического поля вне или внутри магнетика. Не компенсируются только молекулярные токи, выходящие на внешнюю поверхность магнетика. Таким образом, в результате намагничивания парамагнетика можно говорить о некотором поверхностном токе и характеризовать его поверхностной плотностью тока 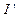(сила тока на единицу длины магнетика). Поверхностный ток создает собственное магнитное поле парамагнетика 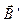, направление которого совпадает с направлением внешнего магнитного поля 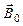. По принципу суперпозиции результирующее поле в парамагнетике

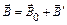. (3.9)

В скалярной форме для однородно намагниченного парамагнетика

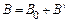. (3.10)

Из (3.10) следует, что 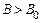, т. е. магнитное поле в парамагнетике больше внешнего поля.

На рис. 43, который является копией рис. 39 для случая парамагнетика, видно, что направление тока 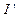по поверхности совпадает с направлением тока в соленоиде, создающем внешнее поле. Токи одинакового направления притягиваются (подразд. 1.1 и 2.3). Таким образом, наличие у атомов парамагнетиков магнитных моментов, отличных от нуля, обусловливает их притяжение к обмотке соленоида, т. е. в область более сильного поля.

Диамагнетики

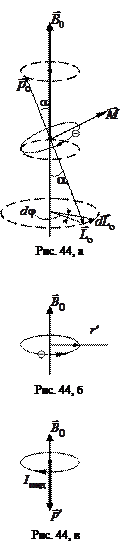В отличие от атома парамагнетика суммарный магнитный момент атома диамагнетика равен нулю. Однако это не означает, что диамагнетики не влияют на магнитное поле. В этом подразделе будет показано, как у диамагнетиков, помещенных в магнитное поле, появляется так называемое индуцированное намагничивание, ослабляющее внешнее магнитное поле.

Рассмотрим движение электрона по круговой орбите радиуса r в атоме, помещенном в магнитное поле с индукцией 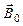(рис. 44, а). Пусть 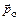– орбитальный магнитный момент электрона, 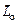– момент импульса электрона. Орбитальное движение электрона можно рассматривать как элементарный контур с током, на который со стороны магнитного поля действует вращательный момент пары сил (2.19):

.

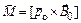С учетом (3.5), получаем

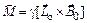. (3.11)

Согласно закону изменения момента импульса [6]

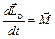. (3.12)

Из (3.11) и (3.12) следует

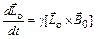. (3.13)

Так как cила Лоренца, действующая на движущийся электрон, работу не совершает (подразд. 2.1), скорость и момент импульса электрона не меняются по величине и магнитное поле приводит только к изменению направления вектора момента импульса. Из (3.13) следует, что вектор 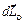перпендикулярен плоскости, содержаще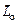й и 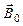. Следовательно, конец вектора 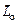движется по окружности, лежащей в плоскости, перпендикулярной 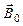(рис. 44, а), и за время 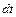перемещается на угол 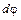, который определяется выражением

.

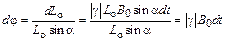Отсюда находим угловую скорость 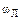движения по окружности конца вектора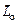

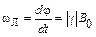. (3.14)

Конец вектора 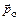, противоположного по направлению вектору 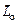, также движется по окружности с угловой скоростью 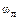. Такому движению векторов 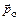и 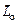соответствует сложное движение электрона: его орбита как бы «катается» по плоскости, перпендикулярной направлению вектора магнитной индукции (рис. 44, а). Это явление в физике получило название прецессия орбиты электрона. Частота прецессии орбиты электрона называется частотой Лармора. Заметим, что частота Лармора не зависит от параметров орбиты или скорости электрона. Она одинакова для всех электронов атома и определяется только величиной магнитной индукции (формула (3.14)).

Сложное движение электрона можно рассматривать как суперпозицию двух движений: по круговой орбите радиуса 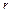вокруг ядра и по окружности радиуса 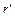в плоскости, перпендикулярной линиям магнитной индукции (рис. 44, б). Второе движение можно трактовать как индуцированный (наведенный) ток. При этом направление индуци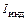рованного тока противоположно направлению движения электрона (рис. 44, в). Соответствующий магнитный момент индуцированного тока 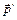направлен противоположно индукции магнитного поля 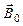(рис. 44, в). Для магнитного момента индуцированного тока справедливо выражение, аналогичное выражению (3.2):

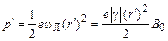. (3.15)

Соотношение (3.15) написано для одного электрона в атоме.

Если диамагнетик находится в магнитном поле, то можно говорить о суммарном индуцированном магнитном моменте атома 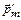, связанном со всеми электронами и направленном противоположно вектору магнитной индукции: 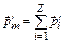, где 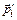– индуцированный магнитный момент i-го электрона в атоме, Z – число электронов в атоме. Пренебрегая магнитным моментом ядра, соотношение (3.1) для магнитного момента атома в магнитном поле можно написать в виде

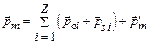. (3.16)

Для диамагнетиков первое слагаемое 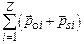равно нулю, поэтому магнитный момент атома определяется только величиной индуцированного магнитного момента 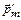, имеющего направление, противоположное направлению вектора магнитной индукции. В этом состоит диамагнитный эффект. Характеристикой намагничивания диамагнетика является вектор намагничивания (подразд. 3.2, формула (3.8)):

.

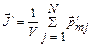Для диамагнетика направление вектора намагничивания противоположно направлению магнитной индукции.

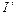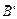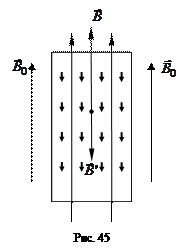
Рассмотрим диамагнетик в форме прямого цилиндра в однородном магнитном поле, расположенный параллельно линиям магнитной индукции. Тогда можно говорить, как и в случае с парамагнетиками (подразд. 3.2), о некотором поверхностном токе и характеризовать его поверхностной плотностью тока . Этот ток создает собственное магнитное поле диамагнетика , направление которого противоположно направлению внешнего магнитного поля 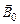(рис. 45). По принципу суперпозиции для результирующего поля в диамагнетике получаем

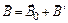. (3.17)

В скалярной форме для однородно намагниченного диамагнетика

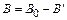. (3.18)

Из (3.18) следует, что 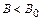, т. е. магнитное поле в диамагнетике меньше внешнего.

На рис. 46, который является копией рис. 39 для случая диамагнетика, видно, что ток 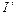по поверхности магнетика и ток в соленоиде противоположны по направлению. А токи противоположного направления отталкиваются (подразд. 1.1 и 2.3). Таким образом, диамагнетик выталкивается в область менее интенсивного поля.

Диамагнитный эффект имеет место у всех веществ. Формула (3.16) справедлива и для парамагнетиков. Однако у парамагнетиков диамагнитный эффект играет второстепенную роль, так как индуцированные магнитные моменты оказываются меньше магнитных моментов атомов парамагнетика:

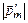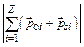
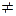< 0.

По этой причине диамагнитным эффектом в парамагнетиках можно пренебречь по сравнению с парамагнитным.