ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ

Настоящее пособие посвящено в основном рассмотрению электрических цепей, в которых сопротивления, индуктивности и емкости не зависят от значений и направлений токов и напряжений. Такие электрические цепи, как и сами элементы, из которых они состоят, называются линейными, так как напряжение и ток в каждом элементе связаны между собой линейным уравнением – алгебраическим или дифференциальным.

Действительно, в случае, если параметр R не зависит от u и i, то закон Ома (1.1) выражает линейную зависимость между напряжением и током.

Если L и С не зависят от u и i, то напряжение и ток связаны линейными дифференциальными уравнениями (1.4) в случае индуктивности и (1.8) в случае емкости.

Что касается активных элементов линейных электрических цепей, то условием линейности идеального источника напряжения является независимость величины ЭДС от тока, проходящего через источник, а условием линейности идеального источника тока является независимость тока от напряжения на его зажимах.

Реальные электротехнические и радиотехнические устройства, строго говоря, не подчиняются линейному закону. При прохождении тока через проводник выделяется тепло, проводник нагревается и его сопротивление изменяется. С изменением тока в катушке индуктивности с ферромагнитным сердечником соотношение между потокосцеплением и током, т. е. параметр L, не остается постоянным. В зависимости от диэлектрика в большей или меньшей степени изменяется и емкость конденсатора в функции от заряда (или приложенного напряжения). К нелинейным устройствам относятся, кроме того, электронные, ионные и полупроводниковые приборы, параметры которых зависят от тока и напряжения.

Если в рабочем диапазоне, на который рассчитывается то или иное устройство, т.е. при заданных ограниченных пределах изменений напряжения, тока и т.п., закон линейности с достаточной для практики степенью точности сохраняется, то такое устройство рассматривается как линейное.

Исследование и расчет линейных цепей сопряжены, как правило, с меньшими трудностями, чем исследование и расчет нелинейных цепей. Поэтому в тех случаях, когда линейный закон достаточно близко отражает физическую действительность, цепь рассматривается как линейная.

В радиоэлектронике и автоматике напряжение и ток, подводимые к цепи, принято называть воздействующей функцией или входным сигналом, а напряжение и ток, возникающие при этом в какой-либо интересующей нас части цепи, называют реакцией цепи или выходным сигналом (в литературе встречается также термин отклик (от английского «respons»)). Сигналы можно рассматривать как функции времени.

В линейной электрической цепи соблюдаются принципы наложения и пропорциональности сигналов.

Принцип наложения заключается в том, что если входным сигналам f_1вх(t) и f_2вх(t), порознь подводимым к цепи, соответствуют выходные сигналы f_1вых(t) и f_2вых(t), то суммарному входному сигналу f_1вх(t) + f_2вх(t) будет соответствовать выходной сигнал f_1вых(t) + f_2вых(t).

Принцип пропорциональности состоит в том, что входному сигналу Аf_вх(t) соответствует выходной сигнал Аf_вых(t), где А - постоянный множитель.

Если с течением времени параметры и схема цепи сохраняются неизменными, то цепь называется инвариантной во времени.

Допустим, что заданная линейная цепь до момента t = 0 пассивна. Условие инвариантности цепи во времени означает, что если входному сигналу f_вх(t) соответствует выходной сигнал f_вых(t), то входному сигналу f_вх(t+t), запаздывающему по сравнению с первым на время t, будет соответствовать выходной сигнал f_вых(t+t).

Отсюда можно заключить, что для линейных электрических цепей, инвариантных во времени, выполняется следующее условие: дифференцирование или интегрирование входного сигнала влечет за собой дифференцирование или соответственно интегрирование выходного сигнала. Действительно, пусть по условию инвариантности входному сигналу f_вх(t+Dt) соответствует выходной f_вых(t+Dt). Если за входной сигнал принять 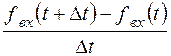, то по условию линейности и инвариантности цепи выходной сигнал будет равен: 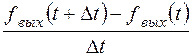. Устремив Dt к нулю в пределе получим входной и выходной сигналы 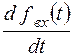и .

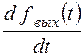Аналогично можно рассмотреть и операцию интегрирования.