Определение численности выборки
Разрабатывая программу выборочного наблюдения, иногда задаются конкретным значением предельной ошибки с уровнем вероятности. Неизвестной остается минимальная численность выборки, обеспечивающая заданную точность. Ее можно получить из формул средней и предельной ошибок в зависимости от типа выборки. Так, подставляя формулы сначала (1.35) и затем (1.36) в формулу (1.38) и решая ее относительно численности выборки, получим следующие формулы
для повторной выборки n =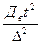 
; (1.41)
для бесповторной выборки n =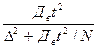 
. (1.42)
Кроме того, при статистических величинах с количественными признаками надо знать и выборочную дисперсию, но к началу расчетов и она не известна. Поэтому она принимается приближенно одним из следующих способов:
— берется из предыдущих выборочных наблюдений;
— по правилу, согласно которому в размахе вариации укладывается примерно шесть стандартных отклонений (R/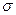 
= 6или R/ 
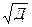= 6; отсюда Д = R2 /36);
— по правилу «трех сигм», согласно которому в средней величине укладывается примерно три стандартных отклонения (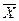 
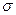/ =3; отсюда 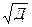= 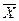/3 или Д = 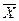2/9).
При изучении не численных признаков, если даже нет приблизительных сведений о выборочной доле, принимается w = 0,5, что по формуле (1.37) соответствует выборочной дисперсии в размере Дв = 0,5(1-0,5) = 0,25.
РЯДЫ ДИНАМИКИ
Дата добавления: 2015-12-26; просмотров: 678;