Аналитическое определение перемещений, аналогов скоростей и ускорений.
Кинематический анализ плоских механизмов
Целью кинематического анализа является определение перемещений,
скоростей и ускорений звеньев или каких-то их точек при заданных размерах и движении ведущего звена.
. Расчёт может быть осуществлён аналитическим или графо-аналитическим методами. Последний метод менее точен, но проще и менее трудоёмок, благодаря чему часто применяется на практике, когда обеспечивает требуемую точность.
При их использовании необходимо по заданным размерам вычертить в масштабе схему механизма в заданном положении (рис.3.1). В данном курсе методика кинематического, силового и динамического расчёта используется для случая кривошипно- ползунного механизма Рассматривается наиболее распространенная схема центрального механизма, в котором линия движения точки В ползуна проходит через центр вращения кривошипа (используется в двигателях внутреннего сгорания). Механизм имеет одну степень свободы: положение всех его подвижных звеньев можно задать с помощью одного независимого параметра (например, угла поворота кривошипа).
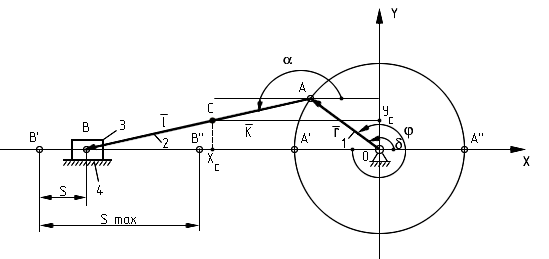
Рис.3.1
Аналитическое определение перемещений, аналогов скоростей и ускорений.
Введем в рассмотрение правую систему координат X, Y с центром в точке O. Ось X параллельна линии движения ползуна. Считаем известными размеры кривошипа OA= 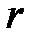 , шатуна AB=
, шатуна AB= 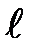 . Направление вращения кривошипа принимаем против часовой стрелки. За один оборот кривошипа ползун перемещается между двумя крайними положениями B' и B'' на величину Smax=
. Направление вращения кривошипа принимаем против часовой стрелки. За один оборот кривошипа ползун перемещается между двумя крайними положениями B' и B'' на величину Smax= 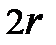 . Величину перемещения S отсчитываем от крайнего левого положения ползуна B' , а величину угла
. Величину перемещения S отсчитываем от крайнего левого положения ползуна B' , а величину угла 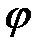 от соответствующего положения кривошипа (OA').
от соответствующего положения кривошипа (OA').
Введем в рассмотрение замкнутый векторный контур OABO. В любом положении механизма выполняется условие:
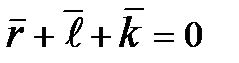 . (3.1) Углы, составленные данными векторами с положительным направлением оси X и отсчитываемые против часовой стрелки, соответственно равны d, a, 0. Спроектируем векторное уравнение (3.1) на оси X, Y:
. (3.1) Углы, составленные данными векторами с положительным направлением оси X и отсчитываемые против часовой стрелки, соответственно равны d, a, 0. Спроектируем векторное уравнение (3.1) на оси X, Y: 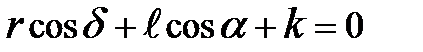 , (3.2)
, (3.2) 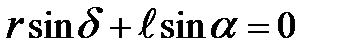 . (3.3)
. (3.3)
Учитывая, что 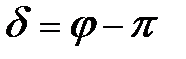 и
и 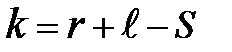 , после преобразований получаем из уравнений (3.2) и (3.3) функции положения шатуна и ползуна ;
, после преобразований получаем из уравнений (3.2) и (3.3) функции положения шатуна и ползуна ;
угол поворота шатуна 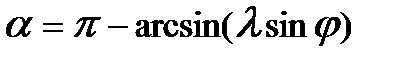 (3.4) перемещение ползуна
(3.4) перемещение ползуна 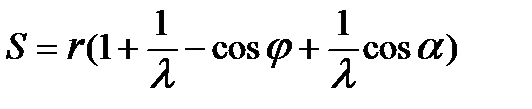 . (3.5) Здесь
. (3.5) Здесь 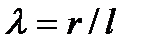 .
.
Определим координаты произвольной точки С шатуна. Ее положение задается расстоянием 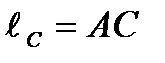 . В векторной форме
. В векторной форме 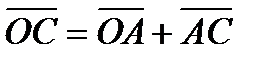 . В проекциях на оси X, Y получаем функции положения точки С.
. В проекциях на оси X, Y получаем функции положения точки С.
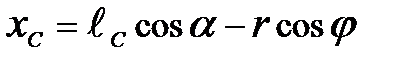 , (3.6)
, (3.6) 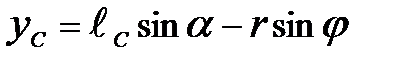 .
.
Дата добавления: 2016-01-26; просмотров: 1545;
