Первая и вторая производные от функции положения по углу называются аналогами скоростей и ускорений.

Найдем зависимости для вычисления аналогов скоростей и ускорений звеньев и точек механизма.

Дифференцируя дважды уравнение (3.4) по 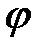, получим выражения для аналогов угловой скорости и углового ускорения шатуна 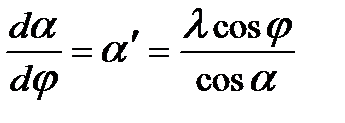; (3.7) 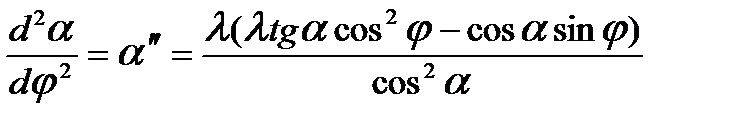. (3.8)

Дифференцируя дважды уравнение (3.5) по 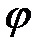, получим зависимости для нахождения аналогов скоростей и ускорений ползуна : 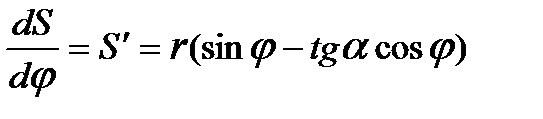(3.9)

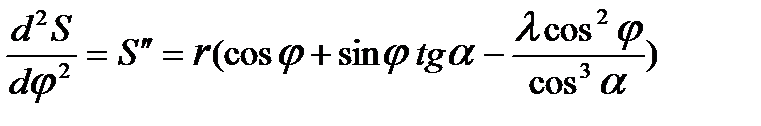. (3.10)

Дифференцируя дважды уравнения (3.6) по 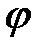, получим в проекциях на оси X,Y выражения аналогов скорости и ускорения произвольной точки С шатуна:

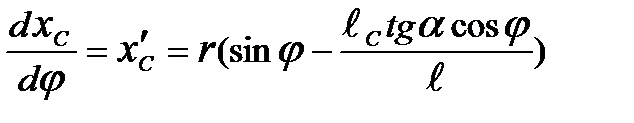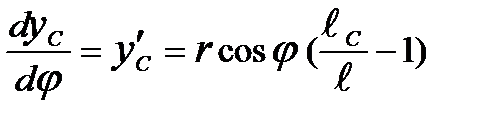; ; (3.11

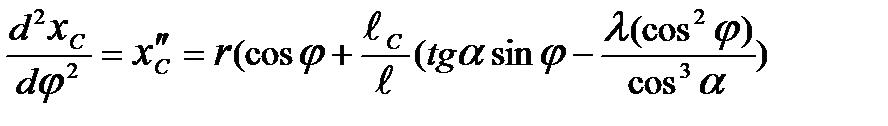); (3.12)

.

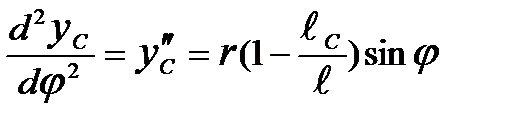При значениях 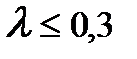для определения перемещения, аналогов скорости и ускорения ползуна можно использовать приближенные завис

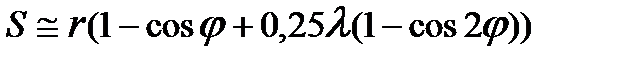. (3.13) 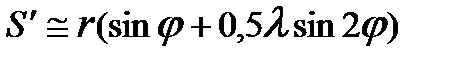. (3.14) . 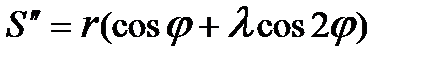(3.15)

Для наглядного представления о характере изменения геометрических и кинематических параметров механизма строятся кинематические диаграммы.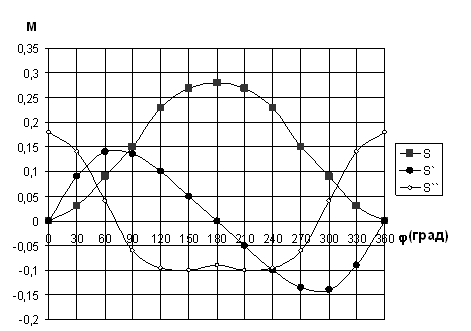

Рис.3.2

При построении необходимо учитывать взаимосвязь между ними, выражающуюся в согласованном расположении характерных точек. Нулевому значению аналога скорости соответствует максимальное (или минимальное) значение перемещения ползуна. Нулевым значениям аналога ускорения соответствуют точки максимума или минимума на графике аналога скорости и точки перегиба на графике перемещения. Точкам максимума или минимума на графике аналога ускорения соответствуют точки перегиба на графике аналога скорости.