Основные аффинные задачи
1. Координаты вектора, заданного двумя точками.
Теорема 1. Если в аффинной системе координат 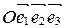
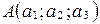 и
и 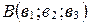 , то
, то 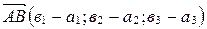 .
.
 Представим вектор
Представим вектор 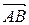 в виде разности векторов
в виде разности векторов 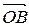 и
и 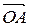 :
:
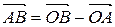 .
.
 Так как
Так как 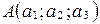 , то по определению координат точки
, то по определению координат точки 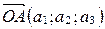 . Аналогично
. Аналогично 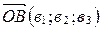 . Применяя свойство координат векторов (координаты разности двух векторов равны разности их соответствующих координат), получаем, что вектор
. Применяя свойство координат векторов (координаты разности двух векторов равны разности их соответствующих координат), получаем, что вектор 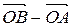 имеет координаты
имеет координаты 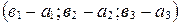 Þ
Þ 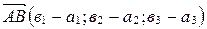 .
.
2. Деление отрезка в данном отношении.
Говорят, что точка М делит направленный отрезок 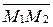 в отношении
в отношении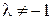 , если выполняется векторное равенство:
, если выполняется векторное равенство:
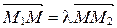 . (1)
. (1)
Число 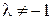 при этом называется простым отношением трех точек М1, М2 и М. Простое отношение трех точек М1, М2 и М обозначается так:
при этом называется простым отношением трех точек М1, М2 и М. Простое отношение трех точек М1, М2 и М обозначается так: 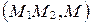 .
.
Почему в определении деления отрезка в данном отношении 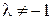 ?
?
Пусть М1 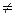 М2 и точка М делит направленный отрезок
М2 и точка М делит направленный отрезок 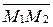 в отношении l=-1. Тогда по определению деления отрезка в данном отношении
в отношении l=-1. Тогда по определению деления отрезка в данном отношении
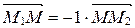 ,
,
т.е. 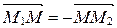 Þ
Þ 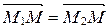 Þ
Þ 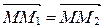 . А так как начало у векторов
. А так как начало у векторов 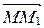 и
и 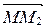 общее и они равны, то М1=М2. Получили противоречие с условием, следовательно,
общее и они равны, то М1=М2. Получили противоречие с условием, следовательно, 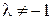 .
.
Из векторного равенства (1) следует, что если 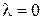 , то
, то 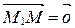 , т.е. точка М совпадает с точкой М1; если l>0, то точка М лежит внутри отрезка
, т.е. точка М совпадает с точкой М1; если l>0, то точка М лежит внутри отрезка 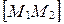 (рис. 36), т.е.
(рис. 36), т.е. 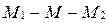 ; если l<0, то точка М лежит на прямой
; если l<0, то точка М лежит на прямой 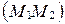 вне отрезка
вне отрезка 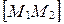 (рис. 37), т.е.
(рис. 37), т.е. 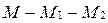 или
или 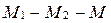 .
.

Теорема 2. Пусть в аффинной системе координат 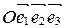
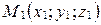 ,
, 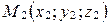 . Тогда координаты точки
. Тогда координаты точки 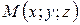 , делящей направленный отрезок
, делящей направленный отрезок 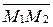 в отношении
в отношении 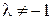 , находятся по формулам:
, находятся по формулам:
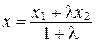 ;
; 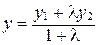 ;
; 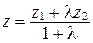 . (2)
. (2)
 По определению деления отрезка в данном отношении
По определению деления отрезка в данном отношении 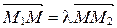 .
.
 По теореме 1
По теореме 1 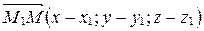 ,
, 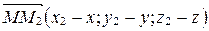 . Тогда
. Тогда 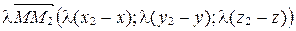 . Так как два вектора равны тогда и только тогда, когда равны их соответствующие координаты, то
. Так как два вектора равны тогда и только тогда, когда равны их соответствующие координаты, то 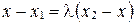 ;
; 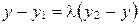 ;
; 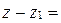

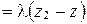 , откуда получаем:
, откуда получаем: 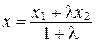 ;
; 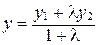 ;
; 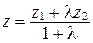 .
.
Формулы (2) называются формулами деления отрезка в данном отношении в координатах.
Из теоремы 2 получаем
Следствие. Если М(х;у;z) – середина отрезка М1М2 с концами 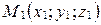 и
и 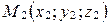 , то
, то 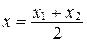 ,
, 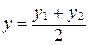 ,
, 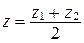 .
.
 Так как М – середина М1М2, то
Так как М – середина М1М2, то 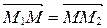 Þ l=1. Применяя формулы деления отрезка в данном отношении в координатах, получаем:
Þ l=1. Применяя формулы деления отрезка в данном отношении в координатах, получаем:

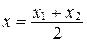 ,
, 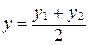 ,
, 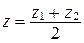 .
.
Дата добавления: 2015-11-28; просмотров: 822;
