Смешанного умножения векторов
Г10. 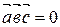
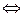
 ,
,  ,
, 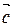 компланарны.
компланарны.
 Пусть
Пусть 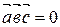 . Тогда
. Тогда 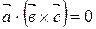
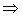
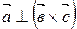 .
.
 По определению векторного произведения
По определению векторного произведения 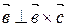 и
и 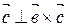 .
.
Следовательно, векторы  ,
,  ,
, 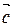 параллельны плоскости, перпендикулярной вектору
параллельны плоскости, перпендикулярной вектору 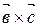 (рис. 24),т.е. векторы
(рис. 24),т.е. векторы  ,
,  ,
, 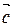 компланарны.
компланарны.
Обратно, пусть векторы  ,
,  и
и 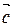 компланарны. Тогда существует плоскость
компланарны. Тогда существует плоскость 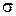 , которой они параллельны.
, которой они параллельны.
 ,
, 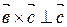 Þ
Þ 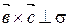 , а так как
, а так как  ||
|| 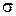 , то
, то 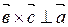 Þ
Þ 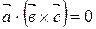 ,
,
 т.е.
т.е. 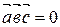 .
.
Г20 (геометрический смысл модуля смешанного произведения). Если векторы  ,
,  ,
, 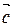 некомпланарны, то абсолютная величина их смешанного произведения равна объему V параллелепипеда с ребрами
некомпланарны, то абсолютная величина их смешанного произведения равна объему V параллелепипеда с ребрами  ,
,  ,
, 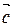 , отложенными от одной точки;
, отложенными от одной точки;  , если тройка
, если тройка  ,
,  ,
, 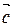 - правая,
- правая, 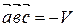 , если тройка
, если тройка  ,
,  ,
, 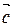 - левая.
- левая.
 Пусть векторы
Пусть векторы  ,
,  ,
, 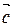 отложены от точки О (рис. 25).
отложены от точки О (рис. 25).
 . Пусть
. Пусть 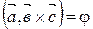 .
.

Построим на векторах 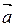 ,
, 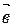 ,
, 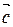 параллелепипед. За основание этого параллелепипеда примем параллелограмм со сторонами
параллелепипед. За основание этого параллелепипеда примем параллелограмм со сторонами 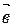 и
и 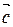 (рис. 26).
(рис. 26).
Пусть n – луч, перпендикулярный основанию параллелепипеда и лежащий в том же полупространстве, что и вектор 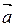 . Пусть h – высота параллелепипеда.
. Пусть h – высота параллелепипеда.

а) Если тройка 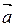 ,
, 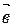 ,
, 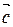 ориентирована так же, как базис
ориентирована так же, как базис 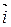 ,
, 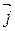 ,
, 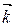 , то
, то 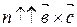 (рис. 26, а) Þ
(рис. 26, а) Þ  < 900 Þ cos
< 900 Þ cos  >0 Þ
>0 Þ 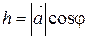 Þ Þ
Þ Þ 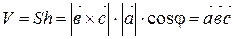 .
.
Итак, 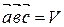 .
.
б) Если тройка 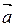 ,
, 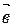 ,
, 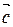 ориентирована противоположно базису
ориентирована противоположно базису 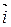 ,
, 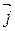 ,
, 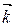 , то
, то  (рис. 26, б) Þ
(рис. 26, б) Þ  > 900 Þ
> 900 Þ 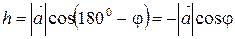 Þ Þ
Þ Þ 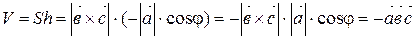 .
.
Итак, 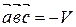 .
.
 Из пунктов а) и б) следует, что
Из пунктов а) и б) следует, что 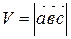 .
.
Дата добавления: 2015-11-28; просмотров: 668;
