Задания для самостоятельной работы. 1. Выясните, каким является базис , , : правым или левым (рис

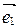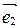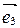1. Выясните, каким является базис , , : правым или левым (рис. 18)?

2. Каким является базис 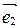, , 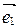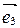: правым или левым (рис. 19)? А базис , , ?

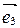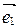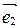3. Начертите на плоскости два различных правых базиса; два различных левых базиса.

Векторное произведение двух векторов

Пусть 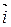, , 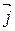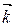- ортонормированный базис трехмерного векторного пространства V (правый). Векторным произведением двух неколлинеарных векторов и называется вектор, обозначаемы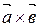й (или 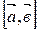) и удовлетворяющий трем условиям:

1) длина ;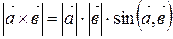

2) 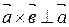и ;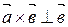

3) базис , , 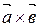ориентирован так же, как базис , , .

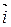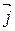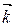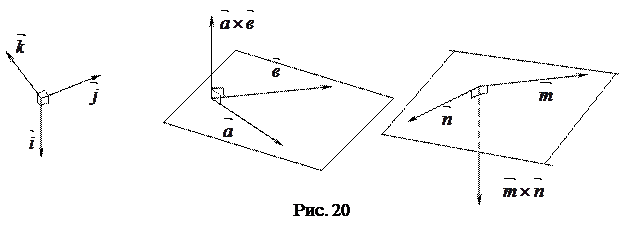Векторным произведением двух коллинеарных векторов называется нулевой вектор.

На рис. 20 изображены векторные произведения 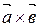и .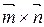

Геометрические свойства

Векторного умножения векторов

Г1⁰. || .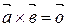

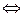
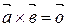Пусть , тогда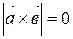

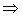
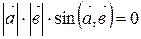
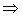
или || ;

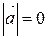
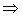
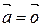
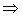
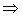или || || ;

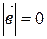
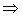
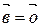
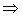
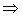
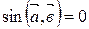
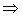
или или || .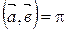

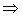
Пусть || . Тогда по определению векторного произведения .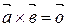

Г2⁰. Длина векторного произведения векторов и равна площади параллелограмма, построенного на этих векторах.

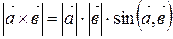По определению . С другой стороны,

(рис. 20).

Следовательно, .

Алгебраические свойства