Скалярное произведение двух векторов

Углом между ненулевыми векторами и называется угол между лучам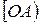и и 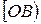, сонаправленными с векторами и соответственно и исходящими из одной точки О (рис. 10).

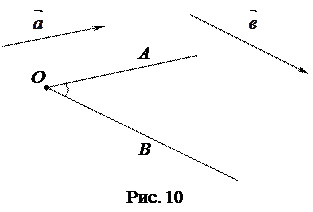Обозначение: .

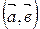Два ненулевых вектора и называются взаимно перпендикулярными (ортогональными), если .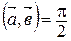

Обозначение: .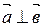

Если хотя бы один из векторов нулевой, то считают, что .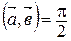

Итак, нулевой вектор ортогонален любому вектору.

Угол между двумя векторами и находится в следующих пределах:

.

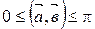Понятие угла между векторами используется при определении понятия скалярного произведения.

Скалярным произведениемдвух векторов называется число (скаляр), равное произведению их длин на косинус угла между ними. Обозначение: 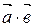или .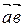

.

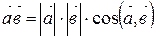Скалярным квадратом вектораназывается число, равное скалярному произведению 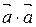. Обозначение: ².

Скалярное умножение векторов не является линейной операцией над векторами.

Скалярное умножение векторов обладает геометрическими и алгебраическими свойствами. В геометрических свойствах фигурируют геометрические величины (длина, угол, перпендикулярность, проекция и т.д.), алгебраические свойства – это свойства, аналогичные свойствам сложения и умножения действительных чисел.