Векторное произведение векторов
Будем предполагать, что пространство является ориентированным. Следуя традиции, считаем, что ориентация задана классом эквивалентности, базисы которого удовлетворяют условию: если их векторы отложены от одной точки, то кратчайший поворот от первого базисного вектора ко второму из конца третьего виден против движения часовой стрелки. Такие базисы мы называем правыми (см. § 6).
Определение 1. Под векторным произведением 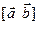 двух неколлинеарных векторов
двух неколлинеарных векторов 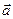 и
и 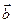 будем понимать третий вектор
будем понимать третий вектор 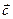 , удовлетворяющий следующим условиям :
, удовлетворяющий следующим условиям :
1. Его модуль равен произведению длин сомножителей, умноженному на синус угла между ними 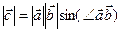
2. Вектор 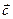 перпендикулярен сомножителям
перпендикулярен сомножителям 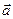 и
и 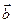 .
.
3. Тройка векторов 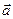 ,
, 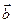 ,
, 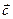 имеет правую ориентацию.
имеет правую ориентацию.
Если векторы 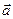 и
и 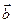 коллинеарны, то их векторное произведение равно нулевому вектору.
коллинеарны, то их векторное произведение равно нулевому вектору.
Свойство1. Если сомножители векторного произведения неколлинеарны, то его длина численно равна площади параллелограмма, построенного на сомножителях.
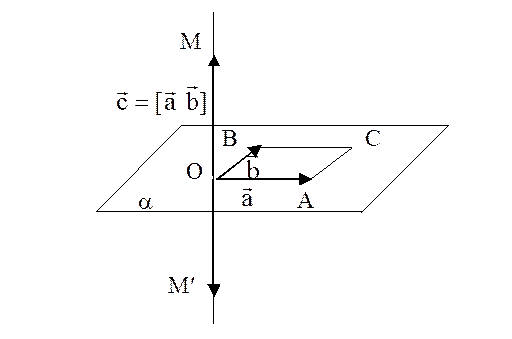 |
Свойство 2. Векторное произведение
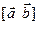 равно нулевому вектору в том случае, когда
равно нулевому вектору в том случае, когда 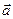 ïï
ïï 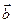 .
.
Свойство 3. Для любых векторов 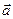 и
и 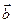 справедливо следующее соотношение:
справедливо следующее соотношение: 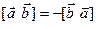 (свойство антикоммутативности).
(свойство антикоммутативности).
Свойство 4. Для любых векторов 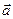 и
и 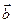 и любого числа
и любого числа 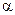 справедливы соотношения:
справедливы соотношения: 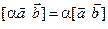
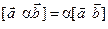 .
.
Свойство 5. Для любых векторов 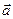 ,
, 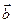 и
и 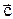 . справедливы соотношения:
. справедливы соотношения:
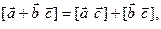
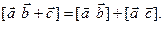
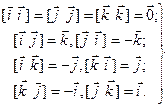
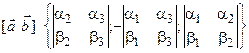
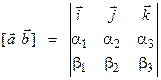
Определение 1. Смешанным произведение векторов 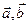 и
и 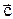 называется скалярное произведение вектора
называется скалярное произведение вектора 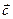 на векторное произведение
на векторное произведение 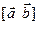 .
.
Смешанное произведение векторов 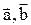 и
и 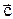 будем обозначать через
будем обозначать через 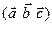 . Итак,
. Итак, 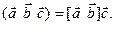
Cвойство 1. Смешанное произведение векторов в том и только в том случае равно нулю, когда сомножители компланарны.
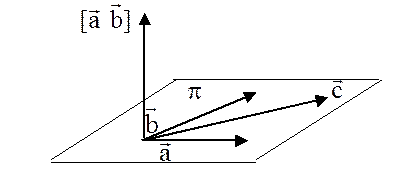
Если векторы 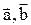 и
и 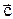 . некомпланарны, то абсолютная величина их смешанного произведения равна объему параллелепипеда, построенного на этих векторах. Смешанное произведение положительно, если тройка векторов
. некомпланарны, то абсолютная величина их смешанного произведения равна объему параллелепипеда, построенного на этих векторах. Смешанное произведение положительно, если тройка векторов 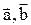 ,
, 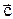 - правая и отрицательно, если эта тройка левая.
- правая и отрицательно, если эта тройка левая.
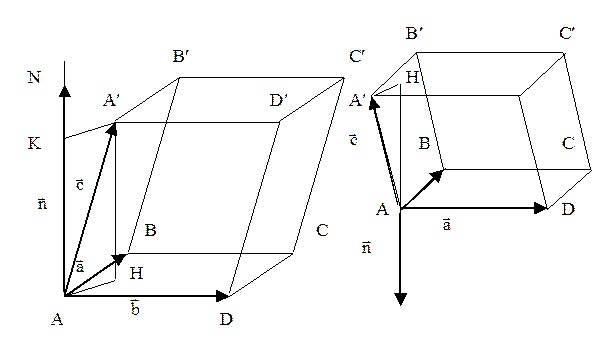 Свойство 3. Для любых векторов
Свойство 3. Для любых векторов 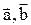 ,
, 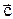 и
и 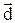 справедливы следующие соотношения:
справедливы следующие соотношения: 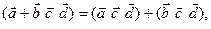
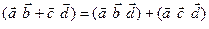 ,
, 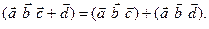
Свойство 4. Для любых векторов 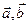 ,
, 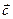 и любого числа a справедливы следующие соотношения:
и любого числа a справедливы следующие соотношения: 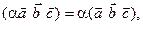
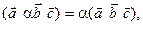
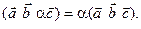
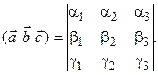
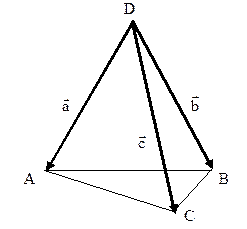 Пример. Противоположные ребра тетраэдра взаимно перпендикулярны между собой. Доказать, что суммы квадратов длин противоположных ребер равны друг другу.
Пример. Противоположные ребра тетраэдра взаимно перпендикулярны между собой. Доказать, что суммы квадратов длин противоположных ребер равны друг другу.
Решение. Пусть АВСD - данный тетраэдр (рис. 37). Обозначим векторы 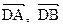 и
и 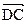 через
через 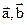 и
и 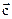 . Тогда
. Тогда 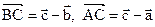 ,
, 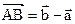 . Нам следует доказать, что
. Нам следует доказать, что 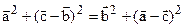 =
= 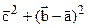 . Рассмотрим равенство:
. Рассмотрим равенство: 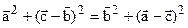 . Докажем справедливость этого соотношения, преобразив его в истинное равенство. Раскроем в этом равенстве скобки:
. Докажем справедливость этого соотношения, преобразив его в истинное равенство. Раскроем в этом равенстве скобки: 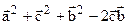 =
= 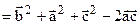 . Отсюда следует, что
. Отсюда следует, что 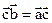 , или
, или 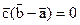 . Последнее равенство является истинным, так как его можно записать в виде
. Последнее равенство является истинным, так как его можно записать в виде 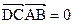 , а по условию нам дано, что противоположные ребра тетраэдра взаимно перпендикулярны. Аналогично доказывается, что
, а по условию нам дано, что противоположные ребра тетраэдра взаимно перпендикулярны. Аналогично доказывается, что 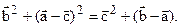
Дата добавления: 2016-02-02; просмотров: 1904;
