Вторая линейная операция – произведение вектор на число
Определение 1. Под произведением ненулевых числа l и вектора 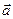 понимается такой вектор
понимается такой вектор 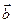 , который удовлетворяет следующим условиям:
, который удовлетворяет следующим условиям:
-
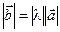 , где
, где 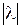 - абсолютная величина l .
- абсолютная величина l . - Если l > 0 , то векторы
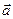 и
и 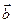 сонаправлены; если l < 0 , то
сонаправлены; если l < 0 , то 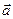 и
и 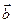 противоположно направлены.
противоположно направлены.
В случае когда l = 0 , либо 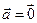 ,произведение
,произведение 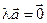 .
.
Свойство 1. Пусть 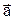 - произвольный вектор, тогда
- произвольный вектор, тогда
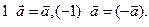 (3.1)
(3.1)
Свойство 2. Для любых чисел a и b. И любого вектора 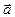 справедливо равенство:
справедливо равенство:
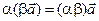 . (3.2)
. (3.2)
Свойство 3. Для любых чисел a и b и любого вектора 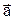 справедливо равенство:
справедливо равенство:
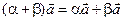 . (3.3)
. (3.3)
Теорема 1. (теорема о коллинеарных векторах). Пусть даны векторы 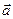 и
и 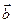 , причем
, причем 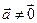 . Они коллинеарны в том и только в том случае, когда существует такое единственное число l., для которого
. Они коллинеарны в том и только в том случае, когда существует такое единственное число l., для которого 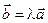 .
.
Свойство 4. Для любого числа a и любых векторов 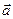 и
и 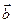 справедливо равенство:
справедливо равенство:
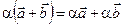
Определение 1. Вектор 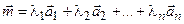 будем называть линейной комбинацией векторов
будем называть линейной комбинацией векторов 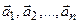 с коэффициентами
с коэффициентами 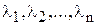 .
.
Определение 2. Система векторов 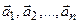 называется линейно зависимой, если существуют такие числа
называется линейно зависимой, если существуют такие числа 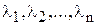 среди которых, по крайней мере, одно отлично от нуля и что линейная комбинация
среди которых, по крайней мере, одно отлично от нуля и что линейная комбинация 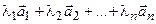 равна нулевому вектору.
равна нулевому вектору.
Если система векторов не является линейно зависимой, то она называется линейно зависимой.
Система 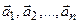 линейно независима в том и только в том случае, когда из равенства
линейно независима в том и только в том случае, когда из равенства 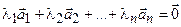 следует:
следует: 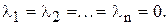
Свойство 1. Если система содержит нулевой вектор, то она линейно зависима.
Свойство 2. Если в системе векторов 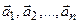 содержится линейно зависимая подсистема, то вся система также линейно зависима.
содержится линейно зависимая подсистема, то вся система также линейно зависима.
Свойство 3. Система векторов линейно зависима тогда и только тогда, когда один из ее векторов линейно выражается через остальные.
Теорема 1. Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.
Компланарные системы векторов. Базис, координаты векторов
Будем говорить, что вектор 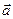 параллелен плоскости
параллелен плоскости 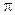 , если его представитель параллелен или лежит в этой плоскости. Ясно, что это определение не зависит от выбора представителя
, если его представитель параллелен или лежит в этой плоскости. Ясно, что это определение не зависит от выбора представителя 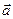 .
.
Определение 3. Система векторов 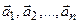 называется компланарной, если существует плоскость, которой параллельны все векторы системы.
называется компланарной, если существует плоскость, которой параллельны все векторы системы.
Примеры компланарной системы векторов:
1. Если система 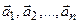 . состоит из коллинеарных векторов, то она компланарная.
. состоит из коллинеарных векторов, то она компланарная.
2. Система, состоящая из двух векторов, всегда является компланарной.
Определение 4. Система, состоящая из двух неколлинеарных векторов плоскости, заданных в определенном порядке, называется базисом плоскости.
Базис будем называть ортонормированным или прямоугольным декартовым, если его векторы взаимно перпендикулярны и имеют единичную длинну. Произвольный базис плоскости называется аффинным или общим декартовым.
(Теорема о разложении вектора плоскости по векторам базиса). Если на плоскости дан базис, то любой ее вектор линейно выражается через векторы базиса, причем коэффициенты разложения определяются единственным образом.
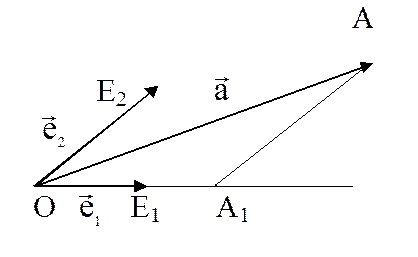
Теорема 3. (Теорема о компланарных векторах).Система, состоящая из трех векторов, линейно зависима тогда и только тогда, когда векторы компланарны.
Следствие.Система, состоящая из трех не компланарных векторов, линейно независима.
Введем основное понятие аналитической геометрии - координаты вектора.
Определение 5.Коэффициенты разложения вектора плоскости по векторам базиса называются координатами этого вектора относительно базиса.
Из теоремы 3 следует, что векторы, составляющие базис пространства, линейно независимы. Базис пространства называется прямоугольным декартовым, если его векторы взаимно перпендикулярны и имеют единичную длину. Произвольный базис пространства носит название аффинного или общего декартова.
Теорема 4. (Теорема о разложении вектора пространства по векторам базиса). Пусть в пространстве дан произвольный базис. Тогда любой вектор пространства линейно выражается через базисные векторы, причем коэффициенты разложения определяются единственным образом.
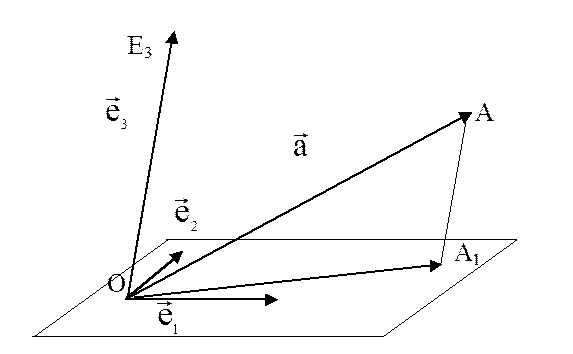
Определение 7.. Коэффициенты разложения вектора пространства по векторам базиса называются его координатами относительно этого базиса.
Теорема.Пусть на плоскости или в пространстве дан базис. Тогда координаты суммы двух векторов равны сумме их соответствующих координат, а координаты произведения вектора на число - произведению этого числа на соответствующие координаты вектора.
Теорема 7. Пусть координаты векторов 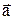 и
и 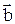 равны
равны 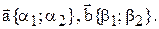 Они коллинеарны в том и только в том случае, когда
Они коллинеарны в том и только в том случае, когда
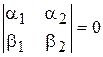 .
.
. Векторы 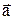 и
и 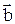 плоскости коллинеарны в том и только в том случае, когда их координаты пропорциональны.
плоскости коллинеарны в том и только в том случае, когда их координаты пропорциональны.
Теорема 8. Два вектора пространства тогда и только тогда коллинеарны, когда их координаты пропорциональны.
Теорема 9. Пусть даны координаты векторов пространства 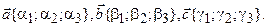 Тогда эти векторы компланарны в том и только в том случае, когда
Тогда эти векторы компланарны в том и только в том случае, когда
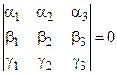 .
.
Дата добавления: 2016-02-02; просмотров: 2593;
