Направленные отрезки и векторы и их свойства.
1. Отрезок называется направленным, если для него указан порядок его концов. Первый из них называется началом, а второй концом направленного отрезка.). Если M начало, а N конец направленного отрезка, то будем его обозначать через  .
.
Определение 1.Направленные отрезки, расположенные на одной прямой или параллельных прямых, называются коллинеарными.
 Определение 2.Если коллинеарные направленные отрезки имеют одинаковые направления, то они называются сонаправленными, если их направления различны, то - противоположно направленными.
Определение 2.Если коллинеарные направленные отрезки имеют одинаковые направления, то они называются сонаправленными, если их направления различны, то - противоположно направленными.
Признак сонаправленности отрезков: пусть  и
и 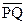 коллинеарные направленные отрезки, не лежащие на одной прямой, они сонаправлены тогда и только тогда, когда их концы N и Q лежат в одной полуплоскости относительно прямой MP, проходящей через их начала (рис. 1 а).
коллинеарные направленные отрезки, не лежащие на одной прямой, они сонаправлены тогда и только тогда, когда их концы N и Q лежат в одной полуплоскости относительно прямой MP, проходящей через их начала (рис. 1 а).
Отсюда следует, что 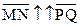 тогда и только тогда, когда отрезки MP и NQ не пересекаются. Если
тогда и только тогда, когда отрезки MP и NQ не пересекаются. Если  и
и  противоположно направлены и не лежат на одной прямой, то их концы N и Q принадлежат различным полуплоскостям относительно прямой MP. Таким образом
противоположно направлены и не лежат на одной прямой, то их концы N и Q принадлежат различным полуплоскостям относительно прямой MP. Таким образом  в том и только в том случае, когда отрезки MP и NQ пересекаются (рис. 1 б).
в том и только в том случае, когда отрезки MP и NQ пересекаются (рис. 1 б).
Направленный отрезок называется нулевым, если его начало совпадает с его концом. У такого отрезка длина равна нулю, считается, что его направление произвольное, т.е. он сонаправлен с любым отрезком.
Определение 3.Два ненулевых направленных отрезка называются равными друг другу, если они сонаправлены и их длины одинаковы. Два нулевых направленных отрезка всегда равны между собой.
Свойство 1. Отношение равенства направленных отрезков является отношением эквивалентности.
Выполняются свойства рефлексивности, симметричности и транзитивности.
 Свойство 2.Отрезок
Свойство 2.Отрезок  равен отрезку
равен отрезку 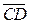 в том и только в том случае, когда середины отрезков AD и BC совпадают (рис. 3).
в том и только в том случае, когда середины отрезков AD и BC совпадают (рис. 3).
Свойство 3. Отрезок  равен отрезку
равен отрезку 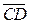 тогда и только тогда, когда
тогда и только тогда, когда 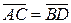 .
.
Свойство 4.Если даны направленный отрезок  и точка С, то существует единственная точка D, для которой
и точка С, то существует единственная точка D, для которой 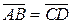 .
.
Определение 4. Вектором называется класс равных между собой направленных отрезков.
Как следует из определения 3, все равные между собой направленные отрезки имеют одну и ту же длину, Её мы будем называть длиной или модулем вектора. и обозначать через 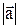 или
или 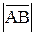 . Модуль нулевого вектора равен нулю.
. Модуль нулевого вектора равен нулю.
Векторы назовем соответственно коллинеарными, сонаправленными или противоположно направленными, если коллинеарны, сонаправлены или противоположно направлены любые два его представителя. Очевидно, что это определение не зависит от выбора представителей векторов. Обозначать коллинеарные, сонаправленные и противоположно направленные векторы будем соответственно через:  Если два вектора имеют одинаковый модуль, но противоположные направления, то их будем называть противоположными. Вектор, противоположный
Если два вектора имеют одинаковый модуль, но противоположные направления, то их будем называть противоположными. Вектор, противоположный 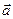 будем обозначать через ( -
будем обозначать через ( - 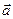 ).
).
Легко видеть, что все нулевые направленные отрезки равны между собой. Действительно, у каждого из них длина равна 0 и они сонаправлены друг с другом. Вектор, представителем которого является нулевой направленный отрезок, называется нулевым. Он будет нами обозначаться через 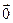 .
.
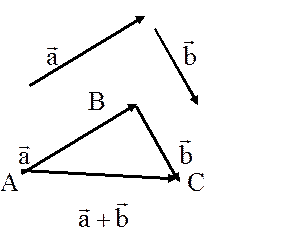
Определение 1.Пусть даны векторы 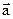 и
и 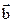 .От точки А отложим вектор
.От точки А отложим вектор 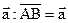 , а от конца направленного отрезка
, а от конца направленного отрезка 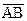 отложим вектор
отложим вектор 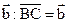 . Вектор
. Вектор 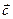 , определенный направленным отрезком
, определенный направленным отрезком 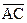 , называется суммой векторов
, называется суммой векторов 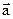 и
и 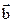 :
: 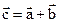 .
.
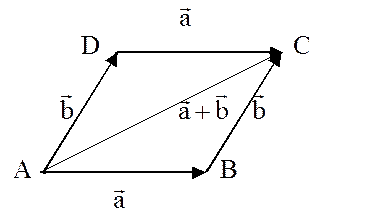 Способ определения суммы векторов - правило параллелограмма.
Способ определения суммы векторов - правило параллелограмма.
 Свойство 1.Для любых векторов
Свойство 1.Для любых векторов 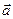 и
и 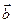 справедливо равенство:
справедливо равенство: 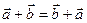 . (свойство коммутативности).
. (свойство коммутативности).
 Свойство 2. Для любых векторов
Свойство 2. Для любых векторов 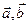 и
и 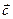 выполнено равенство:
выполнено равенство: 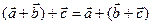 (свойство ассоциативности).
(свойство ассоциативности).
Свойство 3.Для любого вектора 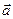 выполнено соотношение:
выполнено соотношение:  .
.
Свойство 4.Для любого вектора 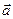 его сумма с противоположным вектором
его сумма с противоположным вектором 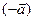 равна нулевому вектору:
равна нулевому вектору:  .
.
Определение 2.Под разностью двух векторов  понимается вектор
понимается вектор 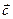 , удовлетворяющий условию:
, удовлетворяющий условию:  .
.
Вектор 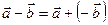
Дата добавления: 2016-02-02; просмотров: 11117;
