Вектор. Основные свойства.
Определение. Вектор – Упорядоченную совокупность  n вещественных чисел называютn-мерным вектором, а числа
n вещественных чисел называютn-мерным вектором, а числа  - компонентами, или координатами, вектора.
- компонентами, или координатами, вектора.
Пример 1.1. Если, например, некоторый автомобильный завод должен выпустить в смену 50 легковых автомобилей, 100 грузовых, 10 автобусов, 50 комплектов запчастей для легковых автомобилей и 150 комплектов для грузовых автомобилей и автобусов, то производственную программу этого завода можно записать в виде вектора (50, 100, 10, 50, 150), имеющего пять компонент.
Обозначения. Векторы обозначают жирными строчными буквами или буквами с чертой или стрелкой наверху, например,aили `a. Два вектора называются равными, если они имеют одинаковое число компонент и их соответствующие компоненты равны.
Компоненты вектора нельзя менять местами, например, (3, 2, 5, 0, 1) ¹
¹ (2, 3, 5, 0, 1).
Операции над векторами. Произведением вектора 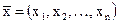 на действительное число l называется вектор
на действительное число l называется вектор 
Суммой векторов 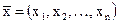 и
и 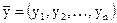 называется вектор
называется вектор 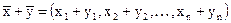 .
.
Пространство векторов. N-мерное векторное пространство Rn определяется как множество всех n-мерных векторов, для которых определены операции умножения на действительные числа и сложение.
Линейная независимость. Система  n-мерных векторов называется линейно зависимой, если найдутся такие числа
n-мерных векторов называется линейно зависимой, если найдутся такие числа 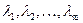 , из которых хотя бы одно отлично от нуля, что выполняется равенство
, из которых хотя бы одно отлично от нуля, что выполняется равенство 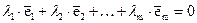 ; в противном случае данная система векторов называется линейно независимой, то есть указанное равенство возможно лишь в случае, когда все
; в противном случае данная система векторов называется линейно независимой, то есть указанное равенство возможно лишь в случае, когда все 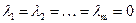 . Геометрический смысл линейной зависимости векторов в R3, интерпретируемых как направленные отрезки, поясняют следующие теоремы.
. Геометрический смысл линейной зависимости векторов в R3, интерпретируемых как направленные отрезки, поясняют следующие теоремы.
Теорема 1. Система, состоящая из одного вектора, линейно зависима тогда и только тогда, когда этот вектор нулевой.
Теорема 2. Для того, чтобы два вектора были линейно зависимы, необходимо и достаточно, чтобы они были коллинеарны.
Теорема 3. Для того, чтобы три вектора были линейно зависимы, необходимо и достаточно, чтобы они были компланарны.
Левая и правая тройки векторов. Тройка некомпланарных векторов 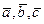 называется правой, если наблюдателю из их общего начала обход концов векторов
называется правой, если наблюдателю из их общего начала обход концов векторов 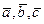 в указанном порядке кажется совершающимся по часовой стрелке. B противном случае
в указанном порядке кажется совершающимся по часовой стрелке. B противном случае 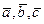 - левая тройка. Все правые (или левые) тройки векторов называются одинаково ориентированными.
- левая тройка. Все правые (или левые) тройки векторов называются одинаково ориентированными.
Базис и координаты. Тройка 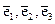 некомпланарных векторов вR3 называется базисом, а сами векторы
некомпланарных векторов вR3 называется базисом, а сами векторы 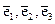 - базисными. Любой вектор
- базисными. Любой вектор  может быть единственным образом разложен по базисным векторам, то есть представлен в виде
может быть единственным образом разложен по базисным векторам, то есть представлен в виде
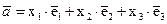 (1.1)
(1.1)
числа 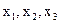 в разложении (1.1) называются координатами вектора
в разложении (1.1) называются координатами вектора  в базисе
в базисе 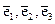 и обозначаются
и обозначаются 
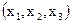 .
.
Ортонормированный базис. Если векторы 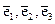 попарно перпендикулярны и длина каждого из них равна единице, то базис называется ортонормированным, а координаты
попарно перпендикулярны и длина каждого из них равна единице, то базис называется ортонормированным, а координаты 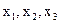 - прямоугольными. Базисные векторы ортонормированного базиса будем обозначать
- прямоугольными. Базисные векторы ортонормированного базиса будем обозначать 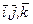 .
.
Будем предполагать, что в пространстве R3 выбрана правая система декартовых прямоугольных координат 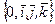 .
.
Пример 1.2.Найдите угол между векторами 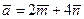 и
и  , где
, где 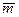 и
и 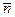 -единичные векторы и угол между
-единичные векторы и угол между 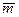 и
и 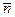 равен 120о.
равен 120о.
Решение. Имеем: 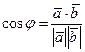 ,
,  ,
, 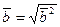
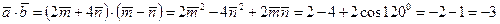
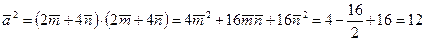 , значит
, значит 
 , значит
, значит 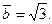
Окончательно имеем: 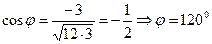 .
.
Пример 1.3.Зная векторы 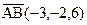 и
и 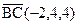 , вычислите площадь треугольника ABC.
, вычислите площадь треугольника ABC.
Решение. Обозначая площадь треугольника ABC через S, получим:
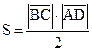 . Тогда
. Тогда 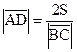 ,
, 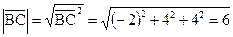 ,
,
Пример 1.4. Даны два вектора 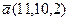 и
и 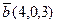 . Найдите единичный вектор
. Найдите единичный вектор 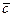 , ортогональный векторам
, ортогональный векторам 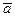 и
и  и направленный так, чтобы упорядоченная тройка векторов
и направленный так, чтобы упорядоченная тройка векторов 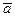 ,
,  ,
, 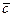 была правой.
была правой.
Решение. Обозначим координаты вектора 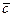 относительно данного правого ортонормированного базиса через
относительно данного правого ортонормированного базиса через 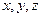 .
.
Поскольку 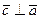 ,
,  , то
, то 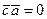 ,
, 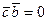 . По условию задачи требуется, чтобы
. По условию задачи требуется, чтобы 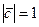 и
и 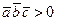 .
.
Имеем систему уравнений для нахождения 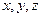 :
:

Из первого и второго уравнений системы получим 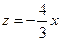 ,
, 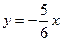 . Подставляя
. Подставляя 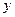 и
и 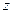 в третье уравнение, будем иметь:
в третье уравнение, будем иметь: 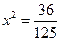 , откуда
, откуда  . Используя условие
. Используя условие 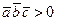 , получим неравенство
, получим неравенство
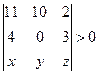 или
или 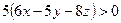
С учетом выражений для 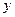 и
и 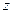 перепишем полученное неравенство в виде:
перепишем полученное неравенство в виде: 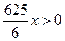 , откуда следует, что
, откуда следует, что 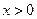 . Итак,
. Итак, 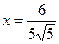 ,
, 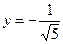 ,
, 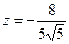 .
.
Дата добавления: 2015-12-22; просмотров: 1392;
