Предел последовательности и функции. Теоремы о пределах
Постоянное число а называется пределом последовательности {xn}, если для любого сколь угодно малого положительного числа e существует номер N, что все значения xn, у которых n>N, удовлетворяют неравенству
êxn - a ê < e. (6.1)
Записывают это следующим образом: 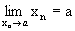 или xn ® a.
или xn ® a.
Неравенство (6.1) равносильно двойному неравенству
a- e < xn < a + e, (6.2)
которое означает, что точки x n, начиная с некоторого номера n>N, лежат внутри интервала (a-e, a+e), т.е. попадают в какую угодно малую e-окрестность точки а.
Последовательность, имеющая предел, называется сходящейся, в противном случае - расходящейся.
Понятие предела функции является обобщением понятия предела последовательности, так как предел последовательности можно рассматривать как предел функции xn = f(n) целочисленного аргумента n.
Пусть дана функция f(x) и пусть a - предельная точка области определения этой функции D(f), т.е. такая точка, любая окрестность которой содержит точки множества D(f), отличные от a. Точка a может принадлежать множеству D(f), а может и не принадлежать ему.
Определение 1. Постоянное число А называется пределом функции f(x) при x®a, если для всякой последовательности {xn} значений аргумента, стремящейся к а, соответствующие им последовательности {f(xn)} имеют один и тот же предел А.
Это определение называют определением предела функции по Гейне, или “на языке последовательностей”.
Определение 2. Постоянное число А называется пределом функции f(x) при x®a, если, задав произвольное как угодно малое положительное число e, можно найти такое d >0 (зависящее от e), что для всех x, лежащих в d-окрестности числа а, т.е. для x, удовлетворяющих неравенству0 < ½x-a½ < d, значения функции f(x) будут лежать в e-окрестности числа А, т.е. êf(x)-A ê < e.
Это определение называют определением предела функции по Коши, или “на языке e - d“.
Определения 1 и 2 равносильны. Если функция f(x) при x ® a имеет предел, равный А, это записывается в виде
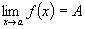 . (6.3)
. (6.3)
В том случае, если последовательность {f(xn)} неограниченно возрастает (или убывает) при любом способе приближения x к своему пределу а, то будем говорить, что функция f(x) имеет бесконечный предел, и записывать это в виде:

Переменная величина (т.е. последовательность или функция), имеющая своим пределом нуль, называется бесконечно малой величиной.
Переменная величина, имеющая бесконечный предел, называется бесконечно большой величиной.
Для нахождения пределов на практике пользуются следующими теоремами.
Теорема 1. Если существуют пределы 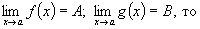
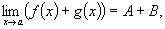 (6.4)
(6.4)
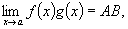 (6.5)
(6.5)
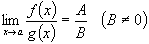 (6.6)
(6.6)
Замечание. Выражения вида 0/0, ¥ /¥, 0 × ¥, ¥ - ¥ являются неопределенными, например, отношение двух бесконечно малых или бесконечно больших величин, и нахождение пределов такого вида носит название “раскрытие неопределенностей”.
Теорема 2.  (6.7)
(6.7)
т.е. можно переходить к пределу в основании степени при постоянном показателе, в частности, 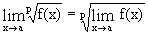 ;
;
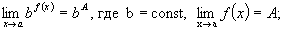 (6.8)
(6.8)
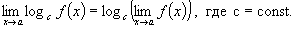 (6.9)
(6.9)
Теорема 3. 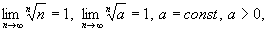
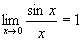 (6.10)
(6.10)
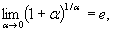 (6.11)
(6.11)
где e » 2.7 - основание натурального логарифма. Формулы (6.10) и (6.11) носят название первого и второго замечательного пределов.
Используются на практике и следствия формулы (6.11):
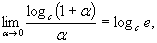 (6.12)
(6.12)
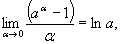 (6.13)
(6.13)
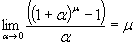 (6.14)
(6.14)
в частности,
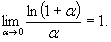
Eсли x® a и при этом x > a, то пишут x® a + 0. Если, в частности, a = 0, то вместо символа 0+0 пишут +0. Аналогично если x®a и при этом x<a, то пишут x®a-0. Числа  и называются соответственно пределом справа и пределом слева функции f(x) в точке а. Для существования предела функции f(x) при x®a необходимо и достаточно, чтобы
и называются соответственно пределом справа и пределом слева функции f(x) в точке а. Для существования предела функции f(x) при x®a необходимо и достаточно, чтобы 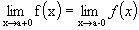 . Функция f(x) называется непрерывной в точке x0, если
. Функция f(x) называется непрерывной в точке x0, если
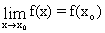 . (6.15)
. (6.15)
Условие (6.15) можно переписать в виде:
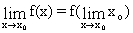 ,
,
то есть возможен предельный переход под знаком функции, если она непрерывна в данной точке.
Если равенство (6.15) нарушено, то говорят, что при x = xo функция f(x) имеет разрыв. Рассмотрим функцию y = 1/x. Областью определения этой функции является множествоR, кроме x = 0. Точка x = 0 является предельной точкой множества D(f), поскольку в любой ее окрестности, т.е. в любом открытом интервале, содержащем точку 0, есть точки из D(f), но она сама не принадлежит этому множеству. Значение f(xo)= f(0) не определено, поэтому в точке xo = 0 функция имеет разрыв.
Функция f(x) называется непрерывной справа в точке xo, если
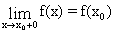 ,
,
и непрерывной слева в точке xo, если
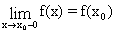 .
.
Непрерывность функции в точке xo равносильна ее непрерывности в этой точке одновременно и справа и слева.
Для того, чтобы функция была непрерывна в точке xo, например, справа, необходимо, во-первых, чтобы существовал конечный предел 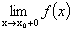 , а во-вторых, чтобы этот предел был равен f(xo). Следовательно, если хотя бы одно из этих двух условий не выполняется, то функция будет иметь разрыв.
, а во-вторых, чтобы этот предел был равен f(xo). Следовательно, если хотя бы одно из этих двух условий не выполняется, то функция будет иметь разрыв.
1. Если 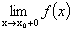 существует и не равен f(xo), то говорят, что функция f(x) в точке xo имеет разрыв первого рода, или скачок.
существует и не равен f(xo), то говорят, что функция f(x) в точке xo имеет разрыв первого рода, или скачок.
2. Если 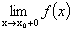 равен ¥ или не существует, то говорят, что в точке xo функция имеет разрыв второго рода.
равен ¥ или не существует, то говорят, что в точке xo функция имеет разрыв второго рода.
Например, функция y = ctg x при x® +0 имеет предел, равный +¥, значит, в точке x=0 она имеет разрыв второго рода. Функция y = E(x) (целая часть от x) в точках с целыми абсциссами имеет разрывы первого рода, или скачки.
Функция, непрерывная в каждой точке промежутка [a,b], называется непрерывной в [a,b]. Непрерывная функция изображается сплошной кривой.
Пример 3.1. Пользуясь определением предела числовой последовательности, доказать, что последовательность xn =(n-1)/n имеет предел, равный 1.
Решение. Нам надо доказать, что, какое бы e>0 мы ни взяли, для него найдется натуральное число N, такое, что для всех n > N имеет место неравенство ½ xn -1 ½<e.
Возьмем любое e >0. Так как ½ xn -1 ½=½(n+1)/n - 1½= 1/n, то для отыскания N достаточно решить неравенство 1/n<e. Отсюда n>1/e и, следовательно, за N можно принять целую часть от 1/e, N = E(1/e). Мы тем самым доказали, что 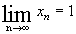 .
.
Пример 3.2. Найти предел последовательности, заданной общим членом 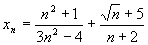 .
.
Решение. Применим теорему о пределе суммы и найдем предел каждого слагаемого. При n ®¥ числитель и знаменатель каждого слагаемого стремится к бесконечности, и мы не можем непосредственно применить теорему о пределе частного. Поэтому сначала преобразуем xn, разделив числитель и знаменатель первого слагаемого на n2, а второго на n. Затем, применяя теорему о пределе частного и о пределе суммы, найдем:
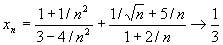 .
.
Пример 3.3. 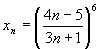 . Найти
. Найти 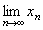 .
.
Решение. 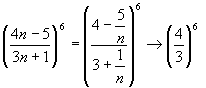 .
.
Здесь мы воспользовались теоремой о пределе степени: предел степени равен степени от предела основания.
Пример 3.4. Найти ( 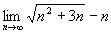 ).
).
Решение. Применять теорему о пределе разности нельзя, поскольку имеем неопределенность вида ¥ - ¥. Преобразуем формулу общего члена:
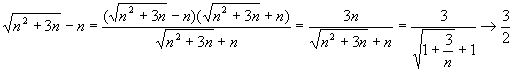 .
.
Пример 3.5. Дана функция f(x)=21/x. Доказать, что 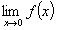 не существует.
не существует.
Решение. Воспользуемся определением 1 предела функции через последовательность. Возьмем последовательность { xn }, сходящуюся к 0, т.е. 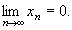 Покажем, что величина f(xn)=
Покажем, что величина f(xn)= 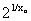 для разных последовательностей ведет себя по-разному. Пусть xn = 1/n. Очевидно, что
для разных последовательностей ведет себя по-разному. Пусть xn = 1/n. Очевидно, что 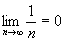 , тогда
, тогда 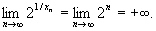 Выберем теперь в качестве xn последовательность с общим членом xn = -1/n, также стремящуюся к нулю.
Выберем теперь в качестве xn последовательность с общим членом xn = -1/n, также стремящуюся к нулю. 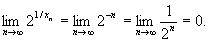 Поэтому
Поэтому 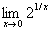 не существует.
не существует.
Пример 3.6. Доказать, что 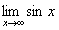 не существует.
не существует.
Решение. Пусть x1, x2,..., xn,... - последовательность, для которой
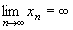 . Как ведет себя последовательность {f(xn)} = {sin xn } при различных xn ®¥ ?
. Как ведет себя последовательность {f(xn)} = {sin xn } при различных xn ®¥ ?
Если xn= pn, то sin xn= sin pn = 0 при всех n и 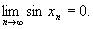 Если же
Если же
xn=2pn+p/2, то sin xn= sin(2pn+p/2) = sin p/2 = 1 для всех n и следовательно  . Таким образом,
. Таким образом, 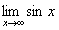 не существует.
не существует.
Пример 3.7. Найти 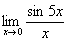 .
.
Решение. Имеем: 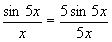 . Обозначим t = 5x. При x®0 имеем: t®0. Применяя формулу (3.10), получим
. Обозначим t = 5x. При x®0 имеем: t®0. Применяя формулу (3.10), получим 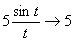 .
.
Пример 3.8. Вычислить  .
.
Решение. Обозначим y=p-x. Тогда при x®p, y®0.Имеем:
sin 3x = sin 3(p-y) = sin (3p-3y) = sin 3y.
sin 4x = sin 4(p-y) = sin (4p-4y)= - sin 4y.
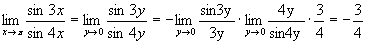 .
.
Пример 3.9. Найти 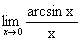 .
.
Решение. Обозначим arcsin x=t. Тогда x=sin t и при x®0 t®0. 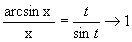 .
.
Пример 3.10. Найти 1) 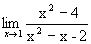 ; 2)
; 2) 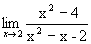 ; 3)
; 3)  .
.
Решение.
1. Применяя теорему 1 о пределе разности и произведения, находим предел знаменателя: 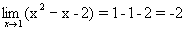 .
.
Предел знаменателя не равен нулю, поэтому, по теореме 1 о пределе частного, получаем: 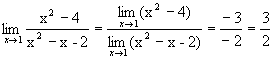 .
.
2. Здесь числитель и знаменатель стремятся к нулю, т.е. имеет место неопределенность вида 0/0. Теорема о пределе частного непосредственно неприменима. Для “раскрытия неопределенности” преобразуем данную функцию. Разделив числитель и знаменатель на x-2, получим при x ¹ 2 равенство:
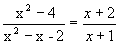
Так как 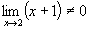 , то, по теореме о пределе частного, найдем
, то, по теореме о пределе частного, найдем
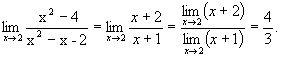
3. Числитель и знаменатель при x®¥ являются бесконечно большими функциями. Поэтому теорема о пределе частного непосредственно не применима. Разделим числитель и знаменатель на x2 и к полученной функции применим теорему о пределе частного:
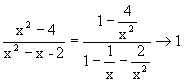 .
.
Пример 3.11. Найти 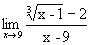 .
.
Решение. Здесь числитель и знаменатель стремятся к нулю: 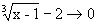 , x-9®0, т.е. имеем неопределенность вида
, x-9®0, т.е. имеем неопределенность вида 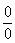 .
.
Преобразуем данную функцию, умножив числитель и знаменатель на неполный квадрат суммы выражения 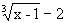 , получим
, получим
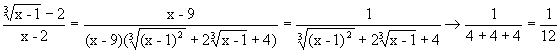 .
.
Пример 3.12. Найти 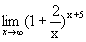 .
.
Решение. 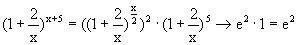 .
.
Дата добавления: 2015-12-22; просмотров: 1573;
