Основные методы интегрирования

Функция F(x), дифференцируемая в данном промежутке X, называется первообразной для функции f(x), или интегралом от f(x), если для всякого x Î X справедливо равенство:

F¢ (x) = f(x). (8.1)

Нахождение всех первообразных для данной функции называется ее интегрированием. Неопределенным интегралом функции f(x) на данном промежутке Х называется множество всех первообразных функций для функции f(x); обозначение -

ò f(x) dx.

Если F(x) - какая-нибудь первобразная для функции f(x), то

ò f(x)dx = F(x) + C, (8.2)

где С - произвольная постоянная.

Непосредственно из определения получаем основные свойства неопределенного интеграла и список табличных интегралов:

1) d ò f(x)=f(x)dx,

2) ò df(x)=f(x)+C,

3) ò af(x)dx=aò f(x)dx (a=const),

4) ò(f(x)+g(x))dx= ò f(x)dx+ ò g(x)dx.

Список табличных интегралов

1. ò x^m dx = x^m+1/(m + 1) +C (m ¹ -1).

2. 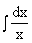= ln êx ê +C.

3. ò a^x dx = a^x/ln a + C (a>0, a¹1).

4. ò e^x dx = e^x + C.

5. ò sin x dx = cos x + C.

6. ò cos x dx = - sin x + C.

7. 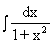= arctg x + C.

8. 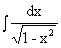= arcsin x + C.

9. 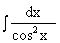= tg x + C.

10. 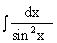= - ctg x + C.

Для интегрирования многих функций применяют метод замены переменной, или подстановки, позволяющий приводить интегралы к табличной форме.

Если функция f(z) непрерывна на [a, b], функция z=g(x) имеет на [a,b] непрерывную производную и a £ g(x) £b, то

ò f(g(x)) g¢ (x) dx = ò f(z) dz, (8.3)

причем после интегрирования в правой части следует сделать подстановку z=g(x).

Для доказательства достаточно записать исходный интеграл в виде:

ò f(g(x)) g¢ (x) dx = ò f(g(x)) dg(x).

Например:

1) ;

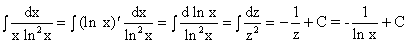2) .

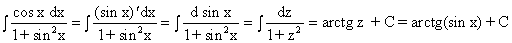Пусть u = f(x) и v = g(x) - функции, имеющие непрерывные производные. Тогда, по правилу дифференцирования произведения,

d(uv)= udv + vdu или udv = d(uv) -vdu.

Для выражения d(uv) первообразной, очевидно, будет uv, поэтому имеет место формула:

ò udv = uv - ò vdu. (8.4)

Эта формула выражает правилоинтегрирования по частям. Оно приводит интегрирование выражения udv=uv'dx к интегрированию выражения vdu=vu'dx.

Пусть, например, требуется найти ò x cosx dx. Положим u = x, dv = cos x dx, так что du=dx, v=sinx. Тогда

ò x cos x dx = ò x d(sin x) = x sin x - ò sin x dx = x sin x + cos x + C.

Правило интегрирования по частям имеет более ограниченную область применения, чем замена переменной. Но есть целые классы интегралов, например,

ò x^k ln^mx dx, ò x^k sin bx dx, ò x^k cos bx dx, ò x^k e ^ax dx

и другие, которые вычисляются именно с помощью интегрирования по частям.

Понятие определенного интеграла вводится следующим образом. Пусть на отрезке [a, b] определена функция f(x). Разобьем отрезок [a, b] на n частей точками a = x₀ < x₁ <...<x_n = b. Из каждого интервала (x_i-1, x_i) возьмем произвольную точку x_i и составим сумму 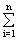f(x_i)D x_i, где
D x_i = x_i - x_i-1. Сумма вида 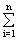f(x_i)D x_i называется интегральной суммой, а ее предел при l = max D x_i ®0, если он существует и конечен, называется определенным интегралом функции f(x) от a до b и обозначается:

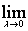
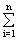f(x_i)D x_i. (8.5)

Функция f(x) в этом случае называется интегрируемой на отрезке
[a, b],числа a и b носят название нижнего и верхнего предела интеграла.

Для определенного интеграла справедливы следующие свойства:

1) ;

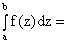
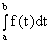2) ;

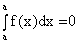3) - ;

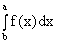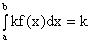
4) 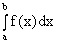, (k = const, kÎR);

5) ;

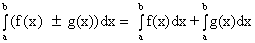6) ;

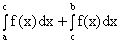7) f(x)(b-a) (xÎ[a,b]).

Последнее свойство называется теоремой о среднем значении.

Пусть f(x) непрерывна на [a, b]. Тогда на этом отрезке существует неопределенный интеграл

ò f(x) dx = F(x) + C

и имеет место формула Ньютона-Лейбница, cвязывающая определенный интеграл с неопределенным:

F(b) - F(a). (8.6)

Геометрическая интерпретация: определенный интеграл 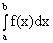представляет собой площадь криволинейной трапеции, ограниченной сверху кривой y= f(x), прямыми x = a и x = b и отрезком оси Ox.