Вероятность и риск, пространство элементарных событий

В этом разделе мы введем некоторые исходные понятия теории вероятностей и начнем работать с математическим аппаратом на несложных примерах. Рассматривая интересующие нас события как элементы множеств, мы можем в дальнейшем производить над ними определенные действия, что поможет нам анализировать совокупность этих событий.

Исторически первой группой случайных событий, которые были исследованы математиками, были азартные игры. Сами правила игры предполагали равноправие участников перед судьбой, при всем мастерстве игрока многое зависело от "везения". Мы также рассмотрим несколько примеров из этой области, т.к. они хорошо иллюстрируют некоторые возможности аппарата теории вероятностей, который пригодится нам в дальнейшем для других случаев. В условиях игры (в карты, в кости) математики и игроки связывают понятие вероятности выигрыша с шансом получения выигрышной комбинации по сравнению с общим числом всех возможных комбинаций.

Пример 4.1.При падении монеты существует два возможных результата (математики называют эти результаты элементарными исходами): выпадет герб или выпадет решетка. Оба результата равновероятны, т.е. вероятность того, что монета останется лежать гербом вверх равна 50% (или 1/2), с такой же вероятностью выпадет другая сторона. Какой бы результат не загадал игрок как благоприятный для себя, его шанс выиграть и вероятность проиграть одинаковы.

Пример 4.2.При бросании игральной кости существует уже шесть возможных элементарных исходов (количество выпавших очков может меняться от 1 до 6). Если игральная кость имеет правильную форму, все шесть результатов равновероятны. Другими словами, вероятность того, что при единственном выбрасывании кости выпадет, например, шесть очков, равна 1/6. Если только эта цифра считается выигрышем при данном броске, шансов выиграть у игрока в три раза меньше, чем в прошлый раз. Если мы хотим "уровнять" шансы при бросании игральной кости с шансом выиграть при бросании монеты, нам надо изменить правила игры, например, считать выигрышем выпадение любого четного числа. Поскольку игральная кость имеет три грани с четными числами и три грани с нечетными, шансы выиграть и проиграть при единственном броске у нас будут одинаковыми (вероятность выигрыша станет равной 1/2, т.е. такой же, как при бросании монеты).

Задание

При подбрасывании монеты вероятность выиграть составляет 1/2, а при бросании игральной кости выигрышем считается выпадение цифры шесть (вероятность выигрыша 1/6). Чему равна вероятность проигрыша в каждом случае?Значит ли это, что играть в кости менее выгодно?

Обсуждение

В каждом из двух случаев вероятность выиграть и проиграть должны составить в сумме 100% или единицу, поскольку ничейный вариант в этих ситуациях невозможен. Это означает, что при бросании монеты вероятность проиграть равна 1/2, а при бросании игральной кости - 5/6. А вот вопрос о "выгодах" предложения поиграть в кости по сравнению с предложением бросить монету не так прост, как это кажется. Оставив на минуту в стороне азартные игры, обсудим одну важную для бизнеса проблему. Решение о "выгодности" любого предпринимаемого нами действия, очевидно, зависит не только от нашей оценки риска данного предприятия, но и от величины предполагаемого выигрыша по сравнению с нашими ставками. Чем меньше шансов получить выигрыш, тем больше должна быть величина этого выигрыша по сравнению со ставкой, чтобы сделать игру привлекательной для потенциальных игроков. Забота о привлекательности условий игры, конечно, распространяется только на те случаи, когда игроки принимают решение об участии в процессе добровольно и осмысленно. Так, чем рискованнее финансовые вложения, тем большую прибыль мы ожидаем получить в результате. Когда соотношение "риск - прибыльность" кажется нам неподходящим, мы ищем возможности покинуть "игру". Поэтому при любой оценке бизнес-проекта оценка рисков не менее важна, чем оценка прибыльности, по сути, это - неотъемлемая часть финансово-экономического анализа. Возвращаясь к нашему заданию, пришло время обсудить финансовые условия игры. Какой именно выигрыш покажется нам справедливым и почему? Если при бросании монеты участвуют два игрока, сделавшие одинаковые ставки, причем выигравший забирает все, то возможный выигрыш в такой игре должен вдвое превышать исходную ставку. Менее очевидный случай - бросание кости. Должен ли выигрыш в шесть раз превышать ставку игрока, и откуда возьмется эта сумма, если игроков по-прежнему только двое? Вот если бы игроков было шестеро, и каждый поставил бы на разную цифру, то при одинаковых исходных ставках получилась бы вполне справедливая игра. Выигравший забрал бы в шесть раз больше, чем поставил, но шансы каждого игрока выиграть были бы одинаковыми. Если же играют двое, причем один выигрывает, только при выпадении цифры "шесть", значит второй выигрывает при любой другой ситуации, и его шансы на выигрыш в пять раз выше. Само по себе это не означает, что игра "нечестная", просто справедливые правила должны потребовать от второго игрока сделать исходную ставку, которая будет в пять раз выше, чем ставка первого игрока. Определение 1. Совокупность всех возможных результатов опыта в теории вероятности называется пространством элементарных исходов, мы будем обозначать это пространство греческой буквой W. Элементарные исходы обозначаются как w_i, где i может принимать значения от одного до максимума по числу возможных вариантов результата опыта. Для наглядности W изображают в виде некоторой области на плоскости, а элементарные исходы wi - точками в этой области. Мы будем также пользоваться математическим обозначением W={wi, i=1, ...} для описания того факта, что пространство элементарных исходов W образуется совокупностью всех элементарных исходов wi. Определение 2.Элементарные исходы могут образовывать группы, каждая из которых называется событием. Событие A, принадлежащее пространству W, (обозначается А М W, см. рисунок), наступает тогда и только тогда, когда наступает один из элементарных исходов wi, входящих в А.

Пример 3. В Примере 2 событием можно считать факт выпадения четной цифры при бросании кости. Это событие наступает, когда выпадает или цифра два, или четыре, или шесть (при трех элементарных исходах из шести возможных). Мы будем пользоваться математическим обозначением А={wi, i=1, ...} для описания того факта, что событие образуется некоторой группой элементарных исходов (напомним, что событие содержится внутри пространства элементарных исходов, как говорят математики, является его подмножеством). В данном примере пространство элементарных исходов W состоит из следующих элементарных исходов:

w1={1}, w2={2}, w3={3}, w4={4}, w5={5}, w6={6}.

Событие А (выпадение четной цифры) можно записать как A={w2, w4, w6}. Иногда говорят, что элементарные исходы w2, w4 и w6 благоприятны для наступления события А, в то время как w1, w3 и w5, напротив, неблагоприятны для него.

Сортировка всего пространства элементарных исходов на благоприятные для интересующего нас события и неблагоприятные, как мы это увидим в следующем разделе, очень важна для нашей оценки вероятности реализации этого события.

Задание.Из трех цифр 1, 2, 3 наудачу берутся две цифры и составляется двузначное число.
Выпишите все элементарные исходы этого опыта. Составьте из элементарных исходов события А, В и С, такие что: А={число содержит цифру 1} В={число содержит только нечетные цифры} С={число четное} Запишите эти события, используя соответствующие математические обозначения.

ОбсуждениеПространство элементарных исходов W состоит из следующих элементарных исходов:w1={12}, w2={21}, w3={13}, w4={31}, w5={23}, w6={32}. Тогда: A={w1, w2, w3, w4} B={w3, w4} C={w1, w6} Отметим, что само пространство элементарных исходов W также представляет собой событие, происходящее всегда (при любом элементарном исходе w). События, от которых в данном эксперименте "никуда не деться", называются достоверными событиями.События называютсянезависимыми, если реализация одного из них не оказывает никакого влияния на вероятность реализации другого. К этому важному свойству мы еще вернемся в следующих разделах. События называются несовместными, если они не могут произойти одновременно. Тоже очень важное свойство, мы встретимся с ним еще не раз.

Пример 4.1.Элементарные исходы являются несовместными событиями при однократном опыте. Например, если мы бросили монету один раз, выпадет или решетка или герб, но, конечно, что-нибудь одно.

В простейшем случае (две стороны одной монеты, шесть граней кубика) вероятность реализации каждого элементарного исхода несложно посчитать из простого здравого смысла. Задача существенно усложняется, если этих элементарных исходов очень много и их приходится определенным образом комбинировать для составления интересующего нас события. Именно в таких более сложных ситуациях на помощь приходит математика. В следующем параграфе мы познакомимся с некоторыми правилами специального раздела математики - комбинаторики.

9.2. Независимость событий. Последовательные события и слепой случай. Теорема умножения вероятностей. "Дерево вероятностей"

При оценке вероятности наступления какого-либо случайного события очень важно предварительно хорошо представлять, зависит ли вероятность наступления интересующего нас события от того, как развиваются остальные события. В случае классической схемы, когда все исходы равновероятны, мы уже можем оценить значения вероятности интересующего нас отдельного события самостоятельно. Мы можем сделать это даже в том случае, если событие является сложной совокупностью нескольких элементарных исходов. А если несколько случайных событий происходит одновременно или последовательно? Как это влияет на вероятность реализации интересующего нас события?

Если я несколько раз кидаю игральную кость, и хочу, чтобы выпала "шестерка", а мне все время не везет, значит ли это, что надо увеличивать ставку, потому что, согласно теории вероятностей, мне вот-вот должно повезти? Увы, теория вероятности не утверждает ничего подобного. Ни кости, ни карты, ни монетки не умеют запоминать, что они продемонстрировали нам в прошлый раз. Им совершенно не важно, в первый раз или в десятый раз сегодня я испытываю свою судьбу. Каждый раз, когда я повторяю бросок, я знаю только одно: и на этот раз вероятность выпадения "шестерки" снова равна одной шестой. Конечно, это не значит, что нужная мне цифра не выпадет никогда. Это означает лишь то, что мой проигрыш после первого броска и после любого другого броска - независимые события.

События А и В называются независимыми, если реализация одного из них никак не влияет на вероятность другого события. Например, вероятности поражения цели первым из двух орудий не зависят от того, поразило ли цель другое орудие, поэтому события "первое орудие поразило цель" и "второе орудие поразило цель" независимы.

Если два события А и В независимы, и вероятность каждого из них известна, то вероятность одновременного наступления и события А, и события В (обозначается АВ) можно посчитать, воспользовавшись следующей теоремой.

Теорема умножения вероятностей для независимых событий: P(AB) = P(A)*P(B) - вероятность одновременного наступления двух независимых событий равна произведениювероятностей этих событий.

Пример.Вероятности попадания в цель при стрельбе первого и второго орудий соответственно равны: р₁=0,7; р₂=0,8. Найти вероятность попадания при одном залпе обоими орудиями одновременно.

Решение: как мы уже видели события А (попадание первого орудия) и В (попадание второго орудия) независимы, т.е. Р(АВ)=Р(А)*Р(В)=р₁*р₂=0,56.

Что произойдет, с нашими оценками, если исходные события не являются независимыми? Давайте немного изменим предыдущий пример.

Пример.Два стрелка на соревнованиях стреляют по мишеням, причем, если один из них стреляет метко, то соперник начинает нервничать, и его результаты ухудшаются. Как превратить эту житейскую ситуацию в математическую задачу и наметить пути ее решения? Интуитивно понятно, что надо каким-то образом разделить два варианта развития событий, составить по сути дела два сценария, две разные задачи. В первом случае, если соперник промахнулся, сценарий будет благоприятный для нервного спортсмена и его меткость будет выше. Во втором случае, если соперник прилично реализовал свой шанс, вероятность поразить мишень для второго спортсмена снижается.

Для разделения возможных сценариев (их часто называют гипотезами) развития событий мы будем часто использовать схему "дерева вероятностей". Эта схема похожа по смыслу на дерево решений, с которым Вам, наверное, уже приходилось иметь дело. Каждая ветка представляет собой отдельный сценарий развития событий, только теперь она имеет собственное значение так называемой условной вероятности (q₁, q₂, q₁-1, q₂-1).

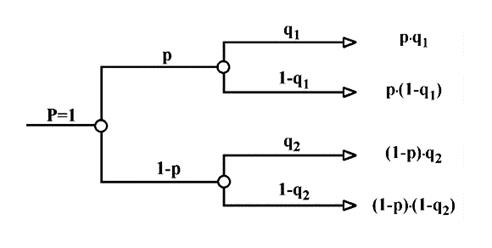
Эта схема очень удобна для анализа последовательных случайных событий.

Остается выяснить еще один немаловажный вопрос: откуда берутся исходные значения вероятностей вреальных ситуациях? Ведь не с одними же монетами и игральными костями работает теория вероятностей? Обычно эти оценки берутся из статистики, а когда статистические сведения отсутствуют, мы проводим собственное исследование. И начинать его нам часто приходится не со сбора данных, а с вопроса, какие сведения нам вообще нужны.

Пример.Допустим, нам надо оценить в городе с населением в сто тысяч жителей объем рынка для нового товара, который не является предметом первой необходимости, например, для бальзама по уходу за окрашенными волосами. Рассмотрим схему "дерева вероятностей". При этом значение вероятности на каждой "ветке" нам надо приблизительно оценить. Итак, наши оценки емкости рынка: 1) из всех жителей города женщин 50%, 2) из всех женщин только 30% красят волосы часто, 3) из них только 10% пользуются бальзамами для окрашенных волос, 4) из них только 10% могут набраться смелости попробовать новый товар, 5) из них 70% обычно покупает все не у нас, а у наших конкурентов.

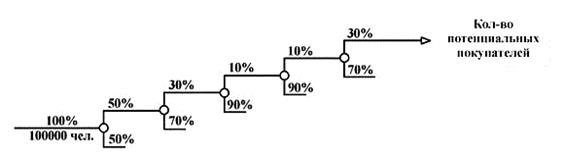
Решение: По закону перемножения вероятностей, определяем вероятность интересующего нас события А={житель города покупает у нас этот новый бальзам}=0,00045. Умножим это значение вероятности на число жителей города. В результате имеем всего 45 потенциальных покупательниц, а если учесть, что одного пузырька этого средства хватает на несколько месяцев, не слишком оживленная получается торговля.

И все-таки польза от наших оценок есть. Во-первых, мы можем сравнивать прогнозы разных бизнес-идей, на схемах у них будут разные "развилки", и, конечно, значения вероятности тоже будут разные. Во-вторых, как мы уже говорили, случайная величина не потому называется случайной, что она совсем ни от чего не зависит. Просто ее точное значение заранее не известно. Мы знаем, что среднее количество покупателей может быть увеличено (например, с помощью рекламы нового товара). Так что имеет смысл сосредоточить усилия на тех "развилках", где распределение вероятностей нас особенно не устраивает, на тех факторах, на которые мы в состоянии повлиять. Рассмотрим еще один количественный пример исследования покупательского поведения.

Пример.За день продовольственный рынок посещает в среднем 10000 человек. Вероятность того, что посетитель рынка заходит в павильон молочных продуктов, равна 1/2. Известно, что в этом павильоне в среднем продается в день 500 кг различных продуктов. Можно ли утверждать, что средняя покупка в павильоне весит всего 100 г?

Обсуждение.Конечно, нельзя. Понятно, что не каждый, кто заходил в павильон, в результате что-то там купил.

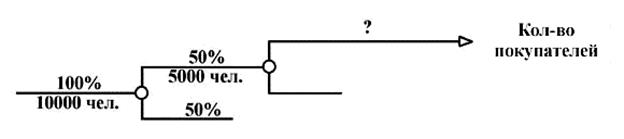Как показано на схеме, чтобы ответить на вопрос о среднем весе покупки, мы должны найти ответ на вопрос, какова вероятность того, что человек, зашедший в павильон, что-нибудь там купит. Если таких данных в нашем распоряжении не имеется, а нам они нужны, придется их получить самим, понаблюдав некоторое время за посетителями павильона. Допустим, наши наблюдения показали, что только пятая часть посетителей павильона что-то покупает. Как только эти оценки нами получены, задача становится уже простой. Из 10000 человек, пришедших на рынок, 5000 зайдут в павильон молочных продуктов, покупок будет только 1000. Средний вес покупки равен 500 грамм. Интересно отметить, что для построения полной картины происходящего, логика условных "ветвлений" должна быть определена на каждом этапе нашего рассуждения так же четко, как если бы мы работали с "конкретной" ситуацией, а не с вероятностями. Задачи для самопроверки 1. Пусть есть электрическая цепь, состоящая из n последовательно соединенных элементов, каждый из которых работает независимо от остальных.

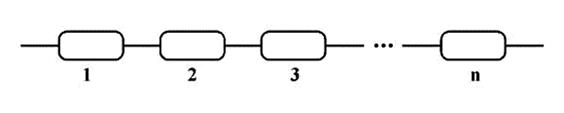
Известна вероятность p невыхода из строя каждого элемента. Определите вероятность исправной работы всего участка цепи (событие А). 2. Студент знает 20 из 25 экзаменационных вопросов. Найдите вероятность того, что студент знает предложенные ему экзаменатором три вопроса. 3. Производство состоит из четырех последовательных этапов, на каждом из которых работает оборудование, для которого вероятности выхода из строя в течение ближайшего месяца равны соответственно р₁, р₂, р₃ и р₄. Найдите вероятность того, что за месяц не случится ни одной остановки производства из-за неисправности оборудования.