НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
Интегралы с бесконечными пределами и интегралы от разрывных (неограниченных) функций называются несобственными. Несобственные интегралы I рода - это интегралы на бесконечном промежутке, определяемые следующим образом:
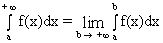 . (8.7)
. (8.7)
Если этот предел существует и конечен, то 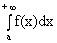 называется сходящимся несобственным интегралом от f(x) на интервале [а,+¥), а функцию f(x) называют интегрируемой на бесконечном промежутке [а,+¥). В противном случае про интеграл
называется сходящимся несобственным интегралом от f(x) на интервале [а,+¥), а функцию f(x) называют интегрируемой на бесконечном промежутке [а,+¥). В противном случае про интеграл 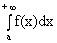 говорят, что он не существует, или расходится.
говорят, что он не существует, или расходится.
Аналогично определяются несобственные интегралы на интервалах
(-¥, b] и (-¥, +¥):
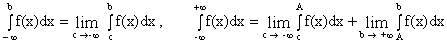 .
.
Определим понятие интеграла от неограниченной функции. Если f(x) непрерывна для всех значений x отрезка [a,b], кроме точки с, в которой f(x) имеет бесконечный разрыв, то несобственным интегралом II рода от f(x) в пределах от a до b называется сумма:
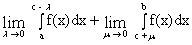 ,
,
если эти пределы существуют и конечны. Обозначение:
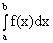 =
= 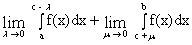 . (8.8)
. (8.8)
Пример 3.29. Вычислить ò dx/(x+2).
Решение. Обозначим t=x+2, тогда dx=dt, ò dx/(x+2) = ò dt/t = lnïtï+C =
= lnïx+2ï+C.
Пример 3.30. Найти ò tg x dx.
Решение. ò tg x dx = ò sin x/cos x dx = - ò d(cos x)/ cos x. Пусть t=cos x, тогда ò tg x dx = - ò dt/t = - lnïtï+C = - lnïcos xï+C.
Пример 3.31. Найти ò dx/sin x.
Решение.
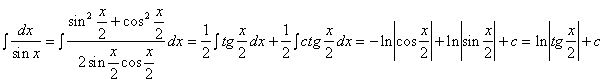
Пример 3.32. Найти 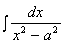 .
.
Решение. 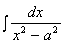 =
= 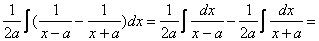
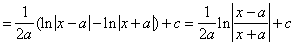
Пример 3.33. Найти ò arctg x dx.
Решение. Обозначим u=arctg x, dv=dx. Тогда du = dx/(x2+1), v=x, откуда ò arctg x dx = x arctg x - ò x dx/(x2+1) = x arctg x + 1/2 ln(x2+1) +C; так как
ò x dx/(x2+1) = 1/2 ò d(x2+1)/(x2+1) = 1/2 ln(x2+1) +C.
Пример 3.34. Вычислить ò ln x dx.
Решение. Применяя формулу интегрирования по частям, получим:
u=ln x, dv=dx, du= 1/x dx, v=x. Тогда ò ln x dx = x lnx - ò x 1/x dx =
= x lnx - ò dx = x lnx - x + C.
Пример 3.35. Вычислить ò ex sin x dx.
Решение. Обозначим u = ex, dv = sin x dx, тогда du = ex dx, v=ò sin x dx= - cos x Þ ò ex sin x dx = - ex cos x + ò ex cos x dx. Интеграл ò ex cos x dx также интегрируем по частям: u = ex, dv = cos x dx Þ du=exdx, v=sin x. Имеем: ò ex cos x dx = ex sin x - ò ex sin x dx. Получили соотношение ò ex sin x dx = - ex cos x + ex sin x - ò ex sin x dx, откуда 2 ò ex sin x dx = - ex cos x + ex sin x + С.
Пример 3.36. Вычислить J = ò cos(ln x)dx/x.
Решение. Так как dx/x = d(ln x), то J= ò cos(ln x)d(ln x). Заменяя ln x через t, приходим к табличному интегралу J = ò cos t dt = sin t + C = sin(ln x) + C.
Пример 3.37. Вычислить J = 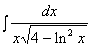 .
.
Решение. Учитывая, что 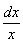 = d(ln x), производим подстановку ln x = t. Тогда J =
= d(ln x), производим подстановку ln x = t. Тогда J = 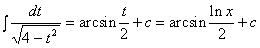 .
.
Пример 3.38. Вычислить интеграл J = 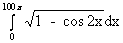 .
.
Решение. Имеем: 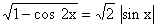 . Поэтому
. Поэтому 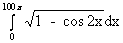 =
=
= 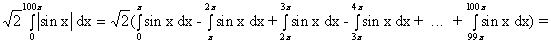
= 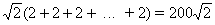 .
.
Пример 3.39.Можно ли применить формулу Ньютона-Лейбница к интегралу 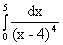 ?
?
Решение. Нет, нельзя. Если формально вычислять этот интеграл по формуле Ньютона-Лейбница, то получим неверный результат. Действительно, 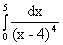 =
= 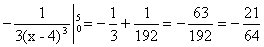 .
.
Но подынтегральная функция f(x) = 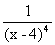 > 0 и, следовательно, интеграл не может равняться отрицательному числу. Суть дела заключается в том, что подынтегральная функция f(x) =
> 0 и, следовательно, интеграл не может равняться отрицательному числу. Суть дела заключается в том, что подынтегральная функция f(x) = 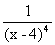 имеет бесконечный разрыв в точке x = 4, принадлежащей промежутку интегрирования. Следовательно, здесь формула Ньютона-Лейбница неприменима.
имеет бесконечный разрыв в точке x = 4, принадлежащей промежутку интегрирования. Следовательно, здесь формула Ньютона-Лейбница неприменима.
Пример 3.40. Вычислить интеграл 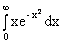 .
.
Решение. Подынтегральная функция определена и непрерывна при всех значениях х и, следовательно, имеет первообразную F(x)= 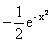 .
.
По определению имеем: 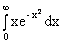 =
= 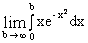 .
.
По формуле Ньютона-Лейбница,
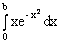 = F(b) - F(0) =
= F(b) - F(0) = 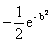 +
+ 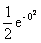 =
=  ;
;
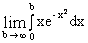 =
= 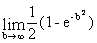 =
=  .
.
Пример 3.44. (Из экономики). При анализе непрерывных потоков платежей предполагалось, что годовая сумма ренты R равномерно распределяется на протяжении года. На практике, особенно в инвестиционных процессах, этот поток может существенно изменяться во времени, следуя какому-либо закону. Если этот поток непрерывен и описывается некоторой функцией
R t = f (t), то общая сумма поступлений за время n равна 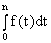 .
.
В этом случае наращенная по непрерывной ставке за период от 0 до n сумма составит:
S = 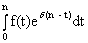 .
.
Современная величина такого потока равна
A = 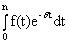 .
.
Пусть функция потока платежей является линейной: Rt = Ro + at, где
Ro - начальная величина платежа, выплачиваемого за единицу времени, в которой измеряется срок ренты. Вычислим современную величину A, пользуясь правилами интегрирования определенного интеграла:
A = 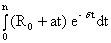 =
= 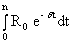 +
+ 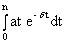 .
.
Обозначим A1 = 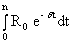 , A2 =
, A2 = 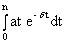 .
.
Имеем: A1 = 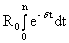 = - Ro/d
= - Ro/d 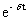 ê
ê 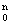 = - Ro/d(
= - Ro/d( 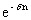 -eo) = - Ro/d(
-eo) = - Ro/d( 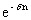 -1) =
-1) =
= Ro( 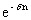 -1)/d. A2 =
-1)/d. A2 = 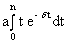 . Вычислим неопределенный интеграл
. Вычислим неопределенный интеграл
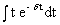 по частям: u = t, dv =
по частям: u = t, dv = 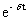 dt Þ du = dt, v =
dt Þ du = dt, v =  = -
= - 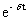 /d, тогда
/d, тогда 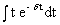 = - t
= - t 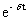 /d + 1/d
/d + 1/d  = - t
= - t 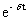 /d (t+1/d) +C. Следовательно,
/d (t+1/d) +C. Следовательно,
A2 = -a t 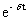 /d (t+1/d)ê
/d (t+1/d)ê 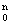 = ((1-
= ((1- 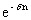 )/d - n
)/d - n 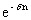 )a/d.
)a/d.
Итак, исходный интеграл
A = A1 + A2 = Ro( 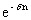 -1)/d + ((1-
-1)/d + ((1- 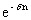 )/d - n
)/d - n 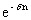 )a/d.
)a/d.
Дата добавления: 2015-12-22; просмотров: 1496;
