Интегралы, не выражающиеся через элементарные функции (не берущиеся).
1. 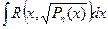 ,где Pn(x) – многочлен n-ой степени; не берется, если n выше 2-ой степени;при n = 2,3,4.. – интеграл эллиптического типа.
,где Pn(x) – многочлен n-ой степени; не берется, если n выше 2-ой степени;при n = 2,3,4.. – интеграл эллиптического типа.
2. 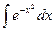 - интеграл Пуассона.
- интеграл Пуассона.
3. 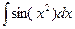 ;
; 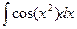 - интегралы Френеля.
- интегралы Френеля.
4. 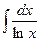 и сводящийся к нему
и сводящийся к нему 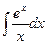 - интегральный логарифм.
- интегральный логарифм.
5. 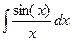 ;
; 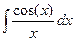 ; - интегральный синус, интегральный косинус.
; - интегральный синус, интегральный косинус.
Раздел II.
Определенный интеграл.
Задача нахождения площади криволинейной трапеции.
Дано: y = f(x) непрерывна на отрезке [a,b]
 y
y

 y=ƒ(x)
y=ƒ(x)
 | |||
 | |||
 ζ1 ζ2 ζi ζn
ζ1 ζ2 ζi ζn
0 a x1 xi-1 xi xn-1 b x
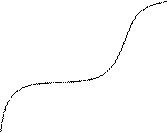
Фигура, ограниченная кривой y=ƒ(x) прямыми x=a и y=b и осью Ox называется криволинейной трапецией.
Найдем площадь:
1) разобьем отрезок [a,b] на n частей точками a = xo < x1 < x2 <…< xi-1 < xi <..< xn = b.
2) через точки деления проведем прямые параллельные оси Оу. В каждом частичном отрезке
[Xo , X1] , [ X1,X2 ] , … [ Xi-1, Xi ] … [ Xn-1, Xn ] выберем произвольные точки
ζ1 ζ2 ζi ζn
Найдем значения функции в этих точках ƒ(ζ1), ƒ(ζ2), ƒ(ζi), ƒ(ζn), и найдем сумму площадей прямоугольников с основанием Δхi = хi – хi-1, i=1,n .
Сумма площадей прямоугольников равна:
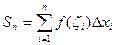 , за площадь криволинейной трапеции принимается предел, к которому стремится эта сумма:
, за площадь криволинейной трапеции принимается предел, к которому стремится эта сумма:
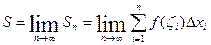 .
.
Дата добавления: 2015-12-16; просмотров: 1367;
