Условие существования определенного интеграла.
Если функция непрерывна на отрезке [a,b], то она интегрируема на этом отрезке.
Замечание: Геометрический смысл интеграла есть площадь криволинейной трапеции.
Sкр.тр.=  .
.
Свойства определенного интеграла.
 1.
1. 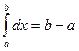 . y
. y

 1
1
 a b x
a b x
2.  =
= 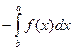 .
.
3. Рассмотрим: интеграл выносится за знак интеграла.
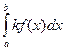 = k
= k  .
.
Доказательство.
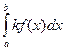 =
= 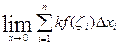 = k
= k 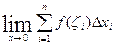 = k
= k  ;
;
4. 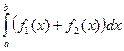 =
= 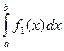 +
+ 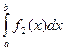 .
.
Доказательство.
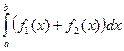 =| по определению| =
=| по определению| = 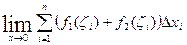 = =
= = 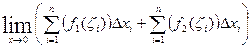 =
= 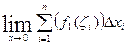 +
+ 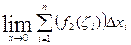 = =
= = 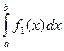 +
+ 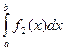 .
.
5. Если [a,b] точкой c делится на 2 отрезок [a,c] и [c,b], то
 =
= 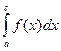 +
+  .
.
Доказательство.
Рассмотрим 1 случай: с между а и b.
Так как определенный интеграл – предел последовательности
 | | | | | | | | | | интеграла суммы, не зависящего от способа
| | | | | | | | | | интеграла суммы, не зависящего от способа
a c b разбиения отрезка на части , то разобьем отрезок на части так, чтобы точка с совпала с точкой разбиения.
Тогда 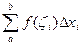 =
= 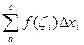 +
+ 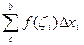 .
.
Перейдем в этом равенстве к пределу при х→0, получим:
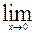
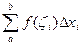 =
= 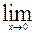
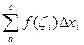 +
+ 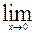
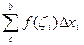 ;
;
 =
= 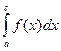 +
+  .
.
2 случай: Пусть с лежит вне отрезка [a,b] a b c
 Тогда по показанному в 1случае, | | |
Тогда по показанному в 1случае, | | |
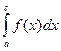 =
=  +
+ 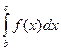 ;
;
Но 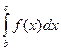 = –
= –  ;
;
Тогда 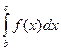 =
=  -
-  ;
;
Отсюда:  =
= 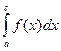 +
+  .
.
6. Если на отрезке [a,b] ƒ(x)≥0 , то  ≥0.
≥0.
Доказательство.
По условию ƒ(ζi)≥0 , Δxi = xi – xi-1 >0;
Тогда 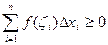
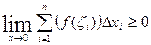 , таким образом,
, таким образом,  ≥0.
≥0.
7. Если на отрезке [a,b] ƒ1(х)≥ ƒ2(х), то 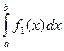 ≥
≥ 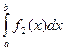 .
.
8. 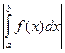 ≤
≤ 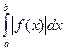 ;
;
Доказательство.
Известно, что – 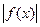 ≤ ƒ(х)≤
≤ ƒ(х)≤ 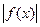 .
.
По свойству 7
– 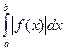 ≤
≤  ≤
≤ 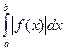 , по свойству абсолютной величины
, по свойству абсолютной величины
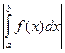 ≤
≤ 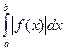 ;
;
9. Если функция y = ƒ(х) непрерывна на отрезке [a,b], то
m(b-a) ≤  ≤ M(b-a)
≤ M(b-a)
Оценка интеграла.
Доказательство.
Так как функция ƒ(х) непрерывна на [a,b], то по свойству непрерывной на отрезке функции, она достигает на этом отрезке своего наименьшего значения m и наибольшего значения M.
Тогда m≤ ƒ(х) ≤ M
По свойству 7: 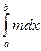 ≤
≤  ≤
≤ 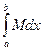 ;
;
По свойству 3: m 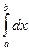 ≤
≤  ≤ M
≤ M 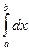 ;
;
По свойству 1: m(b-a) ≤  ≤ M(b-a);
≤ M(b-a);
 |


 Геометрический смысл свойства 9: SM(b-a)
Геометрический смысл свойства 9: SM(b-a)
 | |||
 | |||
m

Sm(b-a)
 a b
a b
Теорема о среднем.
Если функция непрерывна на [a,b], то внутри отрезка найдется по крайней мере одна точка ζ, в которой имеет место равенство:
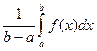 = ƒ(ζ) или
= ƒ(ζ) или
 = (b – a) ƒ(ζ);
= (b – a) ƒ(ζ);
Доказательство.
Так как функция непрерывна на отрезке по свойству 9 имеем:
m(b-a) ≤  ≤ M(b-a);
≤ M(b-a);
разделим на (b-a):
m ≤ 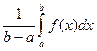 ≤ M;
≤ M;
обозначим 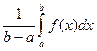 через μ, тогда:
через μ, тогда:
m ≤ μ ≤ M;
Так как функция непрерывна на отрезке [a,b], то по свойству функции, непрерывной на отрезке, она принимает любое значение, по крайней мере в одной точке, данного между m и M.
Значит, найдется такая точка ζ 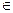 [a, b], в которой функция принимает значение равное μ.
[a, b], в которой функция принимает значение равное μ.
т.е. ƒ(ζ) = μ;
Таким образом 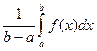 = ƒ(ζ);
= ƒ(ζ);

 Геометрический смысл: ƒ(х)
Геометрический смысл: ƒ(х)




a ζ b
 = ƒ (ζ)(b-a) ;
= ƒ (ζ)(b-a) ;
Площадь криволинейной трапеции равна площади прямоугольника с основанием b-a и высотой, равной значению функции в некоторой «средней» точке ζ.
Дата добавления: 2015-12-16; просмотров: 850;
