Формула Ньютона-Лейбница.
Имеем:
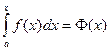 , где Φ(х) – первообразная для функции ƒ(х).
, где Φ(х) – первообразная для функции ƒ(х).
Пусть F(x) - другая первообразная этой функции, тогда
Φ(х) = F(x) + C,
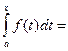 F(x) +C,
F(x) +C,
предположим, в этом равенстве x=a,
получим:
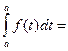 F(a) + C; но
F(a) + C; но 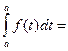 0,
0,
тогда F(a) + C = 0, т.е. С = –F(a);
подставим в исходное значение
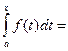 F(x) – F(a), предположим х=b, тогда
F(x) – F(a), предположим х=b, тогда
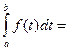 F(b) – F(a), заменим t на х
F(b) – F(a), заменим t на х
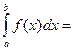 F(b) – F(a) = F(x) |
F(b) – F(a) = F(x) | 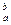 ;
;
Пример: 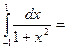 arctg(x) |
arctg(x) | 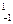 = arctg1 – arctg(-1) = 2arctg1 = 2π/4 = π/2.
= arctg1 – arctg(-1) = 2arctg1 = 2π/4 = π/2.
 Пример2:
Пример2:
Дано: ex , 0≤x≤1,
ƒ(х) = 3-x, 1<x≤3,
 |
построим график функции: y

 2.7
2.7


1 3 х
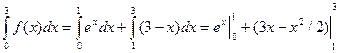 = e –1 + 2 = e+1.
= e –1 + 2 = e+1.
Замена переменной в определенном интеграле.
Пусть функция ƒ(х) непрерывна на отрезке [a,b], а значит существует
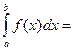 F(b) – F(a), где F(x) первообразная для функции ƒ(х) и пусть х = φ(t), где t
F(b) – F(a), где F(x) первообразная для функции ƒ(х) и пусть х = φ(t), где t 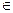 [α,β].
[α,β].
Теорема: Если:
1) φ(α) = а, φ(β) = b.
2) функции φ(t) и φ'(t) непрерывны на отрезке [α,β]
3) функция ƒ(φ(t)) непрерывна на отрезке [α,β],
то 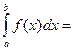
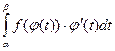 .
.
Доказательство.
В параграфе о замене переменной в неопределенном интеграле было доказано, что функция F(φ(t)) является первообразной для функции ƒ(φ(t))· φ'(t), поэтому
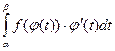 = F (φ(t))
= F (φ(t))  = F(φ(β)) – F(φ(α)) = F(b) – F(a) =
= F(φ(β)) – F(φ(α)) = F(b) – F(a) =  ,
,
что и требовалось доказать.
Пример: Вычислить интеграл:
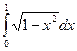 = | x = sin(t),
= | x = sin(t), 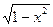 = cos(t), dx = cos(t)dt, при х=0, t=0; при х=1, t = π/2 | =
= cos(t), dx = cos(t)dt, при х=0, t=0; при х=1, t = π/2 | =
= 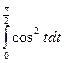 =
= 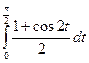 =
= 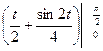 =
= 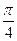 +0 – 0 =
+0 – 0 = 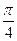 .
.
Пример2:
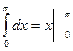 = π;
= π;
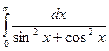 = | tg(x) = t, x = arctg(t) ; dx =
= | tg(x) = t, x = arctg(t) ; dx = 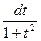 ; sin2x =
; sin2x = 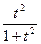 ; cos2x =
; cos2x = 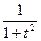 ;
;
при х=0 , t = 0; при х = π, t = 0; | = 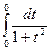 = 0, - это не верно, так как в точке х = π/2, тангенс терпит разрыв.
= 0, - это не верно, так как в точке х = π/2, тангенс терпит разрыв.
Дата добавления: 2015-12-16; просмотров: 665;
