Интегрирование иррациональных функций.
I. Интеграл вида 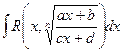 , где
, где 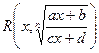 - рациональная функция относительно x и
- рациональная функция относительно x и 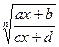 , подстановкой
, подстановкой 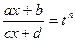 сводится к интегралу от рациональной функции относительно t.
сводится к интегралу от рациональной функции относительно t.
Проверим это.
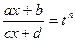 , ax + b = tncx + dtn,
, ax + b = tncx + dtn,
x = 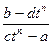 .
.
dx = 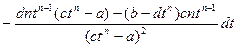 =
= 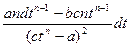 =
= 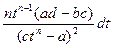 ,
,
т.к. 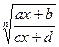 = t , тогда
= t , тогда
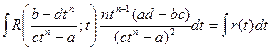 ;
;
r(t)
получаем, что 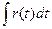 , где r(t)- рациональная функция от t.
, где r(t)- рациональная функция от t.
Замечание:
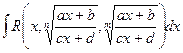 в этом случае заменой
в этом случае заменой
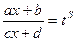 , где s-наименьшее общее кратное чисел m и n.
, где s-наименьшее общее кратное чисел m и n.
Пример: Вычислить интеграл.


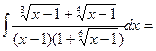 x-1 = t12 , dx = 12t11 dt; =
x-1 = t12 , dx = 12t11 dt; = 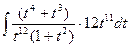 =
=
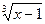 = t4 ;
= t4 ; 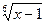 = t2;
= t2;
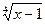 = t3;
= t3;

 = 12
= 12 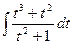 = = 12
= = 12 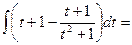 12 ∫t dt +12∫ dt - 12
12 ∫t dt +12∫ dt - 12 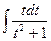 =
=
t3 + t2 |t2 +1
¯ t3 + t t+1
_ t2–t
t2+1
-t-1
= 6t2 + 12t – 6 ∫ (t2+1)-1d(t2 +1) – 12arctg(t) =6t2 + 12t – 6 ln|t2+1| – 12arctg(t) =
= | x –1 =t12 , t = 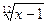 | = 6
| = 6 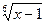 +12
+12 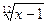 -6ln|
-6ln| 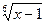 +1| - 12 arctg(
+1| - 12 arctg( 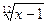 ) + C;
) + C;
II.Интегралы от дифференцированных биномов (биномиальный дифференциал).
Определение : xm(a + bxn)P dx – называется дифференциальным биномом.
Академик Чебышев доказал, что ∫ xm(a + bxn)P dx выражается через элементарные функции в трех случаях:
1) если P-целое, то следует сделать подстановку
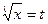 , где λ – общий знаменатель чисел m и n.
, где λ – общий знаменатель чисел m и n.
2)P – не целое, 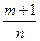 - целое, тогда вводим
- целое, тогда вводим 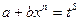 , где s – знаменатель P.
, где s – знаменатель P.
3) P + 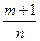 - целое, тогда замена такая:
- целое, тогда замена такая:
ax–n + b = tS , где s – знаменатель P.
В остальных случаях интеграл не берется.
Пример: вычислить интеграл.


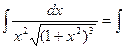 x–2 (1+x2)-3/2 dx = m=-2; n=2; P=-3/2;
x–2 (1+x2)-3/2 dx = m=-2; n=2; P=-3/2; 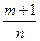 = -
= - 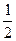 - не целое; =
- не целое; =
P + 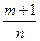 = -1 – целое;
= -1 – целое;

 = x–2 +1 = t2; x–2 = t2 –1; x=( t2 –1)–1/2; = –∫ (t2 –1) (
= x–2 +1 = t2; x–2 = t2 –1; x=( t2 –1)–1/2; = –∫ (t2 –1) ( 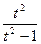 )–3/2 t (t2 –1) –3/2dt=
)–3/2 t (t2 –1) –3/2dt=
dx= -1/2( t2 –1)–3/22tdt = -t ( t2 –1)–3/2dt;
x2 = ( t2 –1)–1= 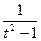 ; 1+ x2 = 1 +
; 1+ x2 = 1 + 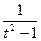 =
= 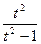
= –∫ (t2 –1) t–2 dt = –∫dt + ∫t–2dt = –t – t-1 = -t –  + C =
+ C = 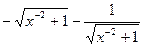 +C =
+C =
= 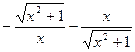 + C;
+ C;
III.Тригонометрические подстановки.
а) Интеграл вида 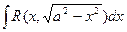 подстановкой x = a∙sin(t) сводится к интегралу от рациональной функции относительно sin(t) и cos(t).
подстановкой x = a∙sin(t) сводится к интегралу от рациональной функции относительно sin(t) и cos(t).


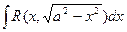 = x=a∙sin(t); dx=acos(t) dt =
= x=a∙sin(t); dx=acos(t) dt = 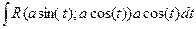 =
=
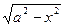 = a∙cos(t); обозначили r(sin(t), cos(t))
= a∙cos(t); обозначили r(sin(t), cos(t))
 =
= 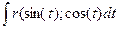 ;
;
рациональная функция относительно sin(t) и cos(t).
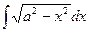 = | x = a∙sin(t); dx = a∙cos(t) | = ∫ a∙cos(t) ∙ a∙cos(t) dt = a2 ∫ cos2(t) dt =
= | x = a∙sin(t); dx = a∙cos(t) | = ∫ a∙cos(t) ∙ a∙cos(t) dt = a2 ∫ cos2(t) dt =
= a2 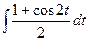 = a2/2 ∫dt + a2/4∫2cos(2t)dt = a2/2 t + a2/4∫cos(2t)d(2t)=a2/2 t + a2/4sin(2t) + C =
= a2/2 ∫dt + a2/4∫2cos(2t)dt = a2/2 t + a2/4∫cos(2t)d(2t)=a2/2 t + a2/4sin(2t) + C =

 = x=a∙sin(t); t = arcsin(x/a); =
= x=a∙sin(t); t = arcsin(x/a); =
sin(2t) = 2sin(t)cos(t) = 2 sin(arcsin(x/a)) cos(arcsin(x/a)) = 2 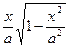
= 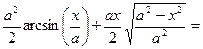
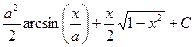 ;
;
 б) интеграл вида
б) интеграл вида 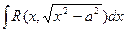 =
=
 = x= a∙ sec(t) = a/cos(t) ;
= x= a∙ sec(t) = a/cos(t) ; 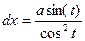 ;
;
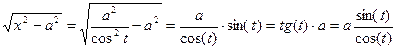 | =
| =
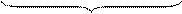 =
= 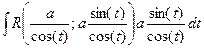 = ∫ r(sin(t), cos(t))dt.
= ∫ r(sin(t), cos(t))dt.
r(sin(t), cos(t))
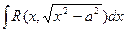 подстановкой x= a∙ sec(t) сводится к интегралу от рациональной функции относительно sin(t) и cos(t).
подстановкой x= a∙ sec(t) сводится к интегралу от рациональной функции относительно sin(t) и cos(t).
в) интеграл вида 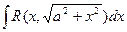 =
=
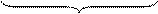

 = x = a∙tg(t) = a
= x = a∙tg(t) = a 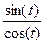 ;
; 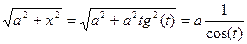 = =
= = 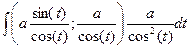 = ∫ r(sin(t), cos(t)) dt.
= ∫ r(sin(t), cos(t)) dt.
r(sin(t), cos(t))
Этот интеграл 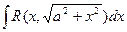 подстановкой x = a∙tg(t) сводится к интегралц от рациональной функции относительно sin(t) и cos(t).
подстановкой x = a∙tg(t) сводится к интегралц от рациональной функции относительно sin(t) и cos(t).
Замечание:
Рассмотрим 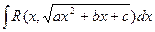 преобразуем в выражение
преобразуем в выражение
ax2+bx+c = a (x2 + 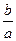 x +
x + 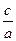 ) = a ((x+
) = a ((x+ 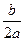 )2 +
)2 + 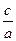 –
– 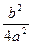 ) = a ((x+
) = a ((x+ 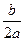 )2 +
)2 + 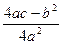 ) ;
) ;
если обозначить x+ 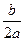 = t ;
= t ; 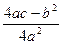 = ± m 2 ;тогда
= ± m 2 ;тогда
ax2+bx+c = a(t2 ± m 2);
x = t – 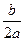 ; dx=dt;
; dx=dt;
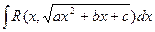 =
=  .
.
Дата добавления: 2015-12-16; просмотров: 921;
