ГРАФИЧЕСКОЕ ИНТЕГРИРОВАНИЕ

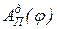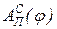При выполнении курсового проекта для определения и построения графиков работ или приведенных моментов сил движущих (для машин-двигателей) или сил сопротивления (для технологических машин) применяется метод графического интегрирования функции приведенного момента сил движущих 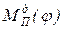или сил сопротивления 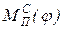, полученной в процессе проектирования в виде графика этого момента.

Рассмотрим этот метод на примере графического интегрирования некоторой функции 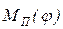, показанной в виде графика на рис. 5, а, и получения графического интеграла 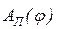(рис.5, б) этой функции.

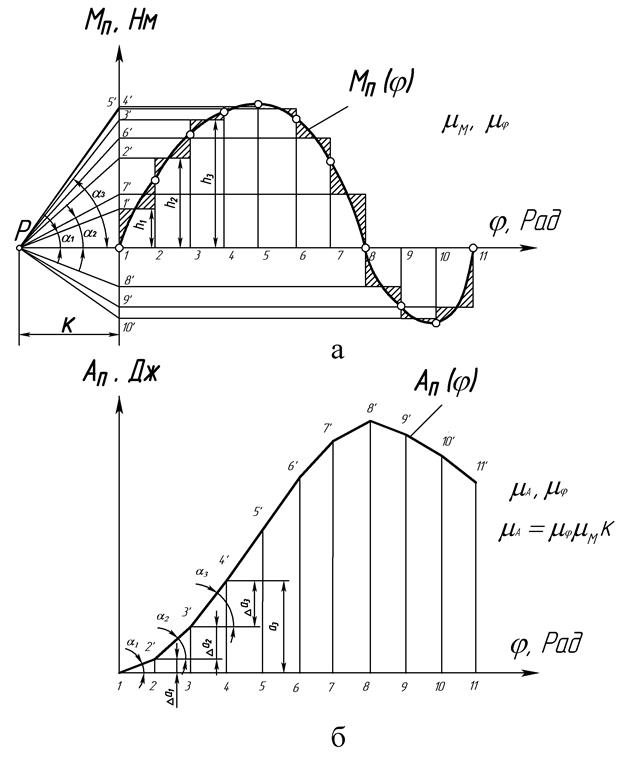
Рисунок 5 – Графическое интегрирование функции М_П(j):

а - график функции М_П(j); б - график функции А_П(j)

При интегрировании ось абсцисс j под кривой 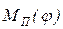разделяется на интервалы интегрирования, через границы которых проводят прямые параллельные оси ординат 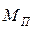до кривой 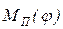. Эти интервалы принимаются относительно небольшими, так как с уменьшением длины интервалов точность интегрирования повышается. На разных участках функции, в зависимости от кривизны ее графика, длины интервалов интегрирования могут быть различны.

При делении на интервалы желательно, чтобы точки пересечения графика 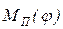с осью абсцисс j, в которых 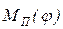= 0, совпадали с границами интервалов (на рис.5, а таковой является точка 8). В этом случае вычисление и построение графика проинтегрированной функции (в данном случае функции 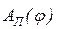) оказывается более точным, так как исключаются ошибки, связанные с переходом интегрируемой (подынтегральной) функции 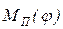из положительной области значений в отрицательную или наоборот. Кроме того, точки пересечения графика 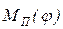с осью абсцисс точно определяют при построении экстремальные значения функции .

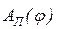Площади под кривой 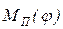на интервалах интегрирования заменяют примерно равными площадями прямоугольников, опирающихся на ось абсцисс. Высоты этих прямоугольников h₁, h₂, h₃ и т.д. определяют их площади, равные в сумме площади под кривой графика 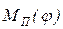на интервале интегрирования. Это условие выполняется при равенстве площадей заштрихованных областей, расположенных по обе стороны графика 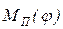выше и ниже горизонтальных сторон прямоугольников. На практике с достаточной точностью равенство этих участков достигается при принятии высоты прямоугольников из условия прохождения горизонтальной стороны через середину участка кривой графика 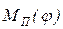на интервалах интегрирования.

Проецируя высоты прямоугольников на графике 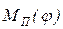на ось 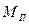ординат, получают на ней точки 1', 2', 3' и т.д. На продолжении оси j абсцисс слева от начала координат на расстоянии К равном30...50 мм отмечают полюс интегрирования – точку Р и соединяют ее лучами с точками 1', 2', 3' и т.д. на оси ординат. Расстояние К определяет масштаб графика 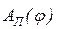(рис.5, б) интегрируемой функции 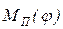. Чем длиннее отрезок интегрирования, тем более пологим будет график результата интегрирования. График 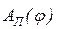строится под графиком 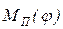с одинаковыми масштабом и интервалами деления оси абсцисс j и через точки деления проводят вертикальные прямые. Из точки 1 начала координат на графике 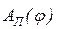(рис.5, б) проводят прямую под углом равным углу a₁ между лучом Р-1' и осью абсцисс на графике 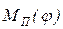(рис.5, б) и на пересечении этой прямой с вертикалью, проведенной через точку 2, получают точку 2'. Из точки 2' проводят прямую под углом равным углу a₂ между лучом Р-2' и осью абсцисс на графике 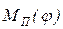и получают точку 3'. Из этой точки проводят прямую под углом a₃ и получают точку 4' и т.д. Соединяя плавной кривой точки 1', 2', 3', 4' и т.д., получают графическое представление функции .

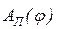График интегрируемой функции 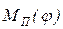строят с масштабным коэффициентом m_М. Масштабный коэффициент m_А графика 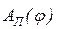зависит от масштабного коэффициента m_М и определяется по следующей методике.

Из графика (рис.5, а) для любого луча Р-i' (Р-1', Р-2' и т.д.) следует

, (46)

где h_i – высота прямоугольника на i-м интервале интегрирования в мм чертежа.

С другой стороны из графика 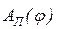(рис.5, б) следует

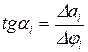, (47)

где 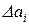– ордината приращения функции А_П(φ) в мм чертежа на i-м интервале; 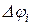– длина интервала в мм чертежа.

Приравнивая значения 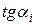из выражений (46), (47), получим

.

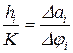Сумма ординат 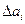представляет собой ординату 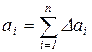. На графике 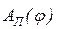(рис.5, б) для трех первых интервалов = + + .

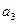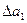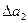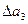Из полученного равенства тангенсов углов a_i следует 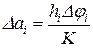, соответственно

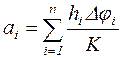. (48)

Параметры, входящие в это соотношение, через масштабные коэффициенты могут быть выражены в виде

, , ,

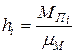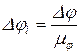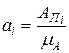где 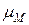, , 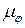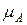– масштабные коэффициенты параметров М_П, j и А_П;

М_Пi – усредненное значение действительного параметра М_П в действительных единицах измерения на i-м интервале интегрирования соответствующее h_i; Dj – значение интервала Dj_i в действительных единицах измерения.

Подставляя значения h_i, Dj_I, и а_i в (48), после преобразований получим

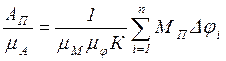. (49)

При графическом интегрировании в процессе выполнения динамического синтеза механизма по заданному коэффициенту неравномерности движения параметры М_П, А_П и j представляют собой соответственно приведенный момент сил, работу этого момента и угол положения звена приведения (кривошипа). В этом случае сумма 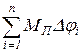в пределе представляет собой 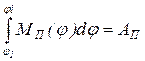, т.е. работу, совершаемую приведенным моментом в течение i интервалов. Подставляя эту сумму в (49), получим выражение для определения масштабного коэффициента 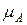в виде

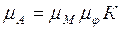. (50)