Дробью или дробно-рациональной функцией.
Если степень числителя меньше степени знаменателя (n<m), то дробь называется правильной, в противном случае (n≥m) называется не правильной.
В случае не правильной дроби, ее можно представить в виде суммы некоторого многочлена и правильной рациональной дроби.
Pn(x) = Mk(x) + Tk(x)
 Qm(x) Qm(x)
Qm(x) Qm(x)
Целая
Часть правильная дробь
Пример: Представить дробь в указанном выше виде.
x5 + 4x ;
x2 + 2x +3
_ x5 + 4x |x2 + 2x +3
x5+2x4+3x3 │x3-2x2+x+4
_ -2x4+4x-3x2-3x3
-2x4+4x3-6x2
_ x3+6x2+4x
x3+2x2+3x
_4x2+x
4x2+8x+12
-7x-12
x5 + 4x = ( x3-2x2+x+4) + -7x-12 ;
x2 + 2x +3 x2 + 2x +3
Теорема1: Если в правильной рациональной дроби знаменатель разложен в виде произведения линейных двучленов и квадратных трехчленов, не имеющих действительных корней:
Q(x) = A0(х- а1)k1(х- а2) k2 …(х- аe) ke (x2 + р1x + q1) t1(x2 + р2x + q2) t2 …(x2 + рsx + qs) ts, то
правильная рациональная дробь разлагается на элементарные дроби по следующей схеме.
P(x) = B1 + B2 +…+ Bk1 + C1 + C2 + … + C k2 + D1 + D2 +…+ D ke +
Q(x) x-a1 (x-a1)2 (x-a1) k1 x-a2 (x-a2)2 (x-a1) k2 x-ae (x-ae) 2 (x-ae) ke
+ E1 x +F1 + E2 x +F2 +…+ Et1 x +Ft1 + M1x +N1 +…+ Mts x +Nts ;
x2 + р1x + q1 (x2 + р1x + q1)2 (x2 + р1x + q1)t1 x2 + рsx + qs (x2 + рsx + qs) ts
Пример: разложить на элементарные дроби следующую дробь:
x2 + x –1 = A + B + C ; где A,B,C – неопределенные коэффициенты.
x(x+1)2 x x+1 (x+1) 2
x2 + x –1 = A(x+1) 2 + Bx(x+1) + C x ;
 I способ.
I способ.
x = -1 -1 = –C; C=1; 1 = -4 + 2B + 1 ;
x = 0 A = -1 ;
x = 1 1 = 4A + 2B + C; B=2;
x2 + x –1 = -1 + 2 + 1 ;
x(x+1)2 x x+1 (x+1) 2
II способ.
x2 + x –1 = A(x+1) 2 + Bx(x+1) + C x ;
x2 + x –1 = x2(A+B) + x(2A+B+C) + A ;
A+B = 1 ; B=2;
2A+b+c = 1; C=1;
A = -1;
Правило интегрирования рациональных дробей:
 1. Если дробь неправильная, то надо выделить целую часть, то есть представить дробь в виде: P(x) = N(x) + T(x)
1. Если дробь неправильная, то надо выделить целую часть, то есть представить дробь в виде: P(x) = N(x) + T(x)
Q(x) Q(x)
 целая
целая
часть правильная дробь.
2. Знаменатель дроби разложить на множители, то есть представить в виде двучленов первой степени и квадратных трехчленов, не имеющих действительных корней. И разложить правильную дробь на элементарные дроби по указанной выше схеме.
3 Интеграл от рациональной дроби взять как сумму интегралов от целой части и от элементарных дробей.
Пример: Найти интеграл.
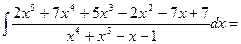 |
|
_ 2x5 + 7 x4 + 5x3 - 2 x2 - 7 x + 7 | x4 + x3 – x –1
2x5 + 2x4 –2x2 -2 x 2x + 5
_ 5x4+5x3–5x+7
5x4+5x3–5x–5
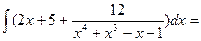 x2 + 5x +12
x2 + 5x +12 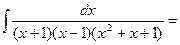

 =
= 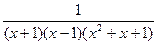 =
= 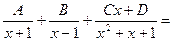
1 = A(x-1)(x2+x+1) + B(x+1)( x2+x+1) + (Cx+D)(x2 – 1)
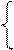 x=1: 1=6B; B=1/6;
x=1: 1=6B; B=1/6;
x=-1: 1=-2A; A=-1/2;
x=0: 0=A+B+C D=2/3; c:=-1/3; =
= x2 + 5x + 12 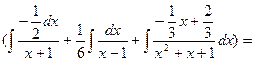 x2 + 5x – 6ln|x+1| + 2ln|x-1| +
x2 + 5x – 6ln|x+1| + 2ln|x-1| +
2 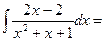 x2 + 5x – 6ln|x+1| + 2ln|x-1| +2
x2 + 5x – 6ln|x+1| + 2ln|x-1| +2 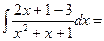 x2 + 5x – 6ln|x+1| + 2ln|x-1| +2
x2 + 5x – 6ln|x+1| + 2ln|x-1| +2 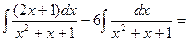 x2 + 5x – 6ln|x+1| + 2ln|x-1| +2ln|x2+x+1| –
x2 + 5x – 6ln|x+1| + 2ln|x-1| +2ln|x2+x+1| –
– 6 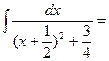 x2 + 5x – 6ln|x+1| + 2ln|x-1| +2ln|x2+x+1| –
x2 + 5x – 6ln|x+1| + 2ln|x-1| +2ln|x2+x+1| – 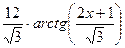 + C.
+ C.
Пример2:


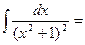
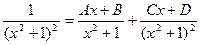 ;
;
1 = Ax3 + Bx2 + Ax + B + Cx + D;
1 = Ax3 + Bx2 + (A+C)x + B + D;
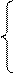 A=0;
A=0;
B=0;
A+C=0; C=0;
B+D=1; D=1;
= 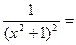 (см. элементарная дробь )
(см. элементарная дробь )
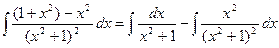 ;
;
Дата добавления: 2015-12-16; просмотров: 731;
